Tìm nghiệm tổng quát của pt sau: 2014x- 2015y +2016 = 0

Những câu hỏi liên quan
Giải phương trình nghiệm nguyên: \(x^2+xy-2014x-2015y-2016=0\)
Lời giải:PT $\Leftrightarrow x^2+x(y-2014)-(2015y+2016)=0$
Coi đây là PT bậc 2 ẩn $x$. Để pt có nghiệm nguyên thì:
$\Delta=(y-2014)^2+4(2015y+2016)=t^2$ với $t\in\mathbb{N}$
$\Leftrightarrow y^2+4032y+4064260=t^2$
$\Leftrightarrow (y+2016)^2+4=t^2$$\Leftrightarrow 4=(t-y-2016)(t+y+2016)$
Đến đây thì đơn giản rồi thì đây là dạng phương trình tích.
Đúng 1
Bình luận (0)
Dùng thuật toán Ơ clit tìm nghiệm nguyên của pt sau : 2014x + 2015y = 4035
HUY - đừng vào câu hỏi của tớ quấy nhiễu
Giải phương trình nghiệm nguyên : \(x^2+2014x+2015y^2+y=xy+2015xy^2+2016\)
chứng minh rằng với số nguyen tố a thì a3 chia hết cho 6
tìm các ngiệm phương trình x2 + xy -2014x -2015y =0
Đề sai rồi bạn, không chia hết cho 6 mà
Đúng 0
Bình luận (0)
Bạn lai lịch bất thường nhỉ? Lúc hỏi câu lớp 6 lúc thì câu lớp 9, bạn học không kịp CT à
Đúng 0
Bình luận (0)
chứng minh rằng với số nguyen tố a thì a3 chia hết cho 6
tìm các ngiệm phương trình x2 + xy -2014x -2015y =0
cho x y>0 và x+y=2016/2015. tìm GTNN của S=2015/x+1/2015y
cho x y>0 và x+y=2016/2015. tìm GTNN của S=2015/x+1/2015y
\(S=2015\left(\frac{1}{x}+x\right)+\left(\frac{1}{2015y}+2015y\right)-2015\left(x+y\right)\)
\(\ge2015.2\sqrt{\frac{1}{x}.x}+2\sqrt{\frac{1}{2015y}.2015y}-2015.\frac{2016}{2015}\)
\(=2.2015+2-2016=2016\)
Đẳng thức xảy ra khi x = 1; y = 1/2015.
Đúng 0
Bình luận (0)
a)Tìm nghiệm tổng quát của pt: 2x+y=5
b)Trong các cặp số(-2;1)và (0;2) cặp số nào là nghiệm của pt:5x+4y=8? Vì sao?
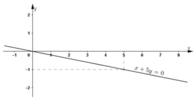
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó: x + 5y = 0
x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
Đúng 0
Bình luận (0)

















