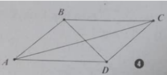
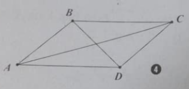
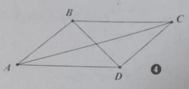
Cho hình bình hành ABCD, tìm ảnh của B qua phép tịnh tiến AD

Những câu hỏi liên quan
Cho hình vuông ABCD có tâm I.
a.Xác định hình H1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo vecto AI.
b. Xác định hình H2 là ảnh H1 qua phép tịnh tiến vecto IB.
c. Có 1 phép tịnh tiến nào biến H2 thành hình vuông ABCD.
Cho hình bình hành ABCD. Phép tịnh tiến
T
A
B
→
+
A
D
→
biến điểm A thành điểm: A. A’ đối xứng với A qua C B. A’ đối xứng với D qua C C.O là giao điểm của AC và BD D. C
Đọc tiếp
Cho hình bình hành ABCD. Phép tịnh tiến T A B → + A D → biến điểm A thành điểm:
A. A’ đối xứng với A qua C
B. A’ đối xứng với D qua C
C.O là giao điểm của AC và BD
D. C
Cho hình bình hành ABCD. Phép tịnh tiến
T
A
B
→
+
A
D
→
biến điểm A thành điểm: A. A’ đối xứng với A qua C B. A’ đối xứng với D qua C C.O là giao điểm của AC và BD D. C
Đọc tiếp
Cho hình bình hành ABCD. Phép tịnh tiến T A B → + A D → biến điểm A thành điểm:
A. A’ đối xứng với A qua C
B. A’ đối xứng với D qua C
C.O là giao điểm của AC và BD
D. C
Cho hình vuông ABCD, gọi O là giao điểm của AC và BD. Tìm ảnh của các điểm A, B, O qua phép đối xứng tâm O góc 90 ° ; phép tịnh tiến AB
Bài 1: Cho hình vuông ABCD tâm I. Gọi M,N lần lượt là trung điểm của AD, DC.Tìm phép tịnh tiến biến Delta AMI thành Delta MDN.Bài 2: Cho hình bình hành ABCD. Trình bày các phép tình tiến biến đường thẳng AB thành đường thẳng CD và biến đường thẳng AD thành đường thẳng BC.Bài 3: Trong mặt phẳng tọa độ Oxy, cho Delta ABC biết A(2;4), B(5;1), C(-1;-2). Phép tình tiến theo véctơ overrightarrow{BC} biến Delta ABC thành Delta ABC tương ứng các điểm. Tìm tọa độ trọng tâm G của Delta ABC.
Đọc tiếp
Bài 1: Cho hình vuông ABCD tâm I. Gọi M,N lần lượt là trung điểm của AD, DC.Tìm phép tịnh tiến biến \(\Delta AMI\) thành \(\Delta MDN\).
Bài 2: Cho hình bình hành ABCD. Trình bày các phép tình tiến biến đường thẳng AB thành đường thẳng CD và biến đường thẳng AD thành đường thẳng BC.
Bài 3: Trong mặt phẳng tọa độ Oxy, cho \(\Delta ABC\) biết A(2;4), B(5;1), C(-1;-2). Phép tình tiến theo véctơ \(\overrightarrow{BC}\) biến \(\Delta ABC\) thành \(\Delta A'B'C'\) tương ứng các điểm. Tìm tọa độ trọng tâm G' của \(\Delta A'B'C'\).
Cho hình bình hành ABCD. Phép tịnh tiến T D A → biến:
A. B thành C
B. C thành A
C. C thành B
D. A thành D
Cho hình bình hành ABCD. Phép tịnh tiến T D A → biến:
A. B thành C
B. C thành A
C. C thành B
D. A thành D
Cho hình vuông ABCD tâm O .Hãy dựng hình vuông A ' B' C' D' là ảnh của hình vuông ABCD qua phép tịnh tiến theo vector AO
Cho hình bình hành ABCD tâm O : a) Tìm ảnh của các điểm A , B , C , D và đường thẳng AB qua phép tịnh tiến vecto vAB b) Tìm ảnh của các điểm A,B,C,D qua phép tịnh tiến vecto v AO c) Tìm ảnh của các điểm A,B,C qua phép tịnh tiến vecto vOC Vẽ hình kèm lời giải hộ mình nha❤️❤️❤️
Đọc tiếp
Cho hình bình hành ABCD tâm O : a) Tìm ảnh của các điểm A , B , C , D và đường thẳng AB qua phép tịnh tiến vecto v=AB b) Tìm ảnh của các điểm A,B,C,D qua phép tịnh tiến vecto v= AO c) Tìm ảnh của các điểm A,B,C qua phép tịnh tiến vecto v=OC Vẽ hình kèm lời giải hộ mình nha❤️❤️❤️
Câu 1: Cho hình bình hành ABCD. Phép tịnh tiến T_{overrightarrow{DA}} biếnA. B thành CB. C thànhBC. C thành AD. A thành DCâu 2: Cho hình bình hành ABEF. Gọi D,C lần lượt là trung điểm của AF và BF, O là giao điểm của AC và BD, I là giao điểm của FC và DE. Phép tịnh tiến T_{overrightarrow{FI}} biến tam giác DIF thành tam giác nào sau đây:A. Delta AODB. Delta CIEC. Delta OBCD. Delta OCICâu 3: Trong mặt phẳng, phép tịnh tiến T_{overrightarrow{v}}left(Aright)B và T_{overrightarrow{v}}left(Cright)D ...
Đọc tiếp
Câu 1: Cho hình bình hành ABCD. Phép tịnh tiến \(T_{\overrightarrow{DA}}\) biến
A. B thành C
B. C thànhB
C. C thành A
D. A thành D
Câu 2: Cho hình bình hành ABEF. Gọi D,C lần lượt là trung điểm của AF và BF, O là giao điểm của AC và BD, I là giao điểm của FC và DE. Phép tịnh tiến \(T_{\overrightarrow{FI}}\) biến tam giác DIF thành tam giác nào sau đây:
A. \(\Delta AOD\)
B. \(\Delta CIE\)
C. \(\Delta OBC\)
D. \(\Delta OCI\)
Câu 3: Trong mặt phẳng, phép tịnh tiến \(T_{\overrightarrow{v}}\left(A\right)=B\) và \(T_{\overrightarrow{v}}\left(C\right)=D\) với \(\left(\overrightarrow{v}\ne\overrightarrow{0}\right)\) Mệnh đề nao sau đây sai?
A. \(\overrightarrow{AC}=\overrightarrow{BD}\)
B. \(\overrightarrow{AB}=\overrightarrow{CD}\)
C. \(\overrightarrow{AD}=\overrightarrow{CB}\)
D. \(AB=CD\)
Câu 4: Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow{v}=\left(3;1\right)\). Tìm tọa độ của điểm \(M'\) là ảnh của điểm \(M\left(-2;1\right)\) qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
A. \(M'\left(5;0\right)\)
B. \(M'\left(1;2\right)\)
C. \(M'\left(-5;0\right)\)
D. \(M'\left(5;2\right)\)
Câu 5: Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(-2;1\right)\). Tìm tọa độ điểm N sao cho M là ảnh của N qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}=\left(-3;2\right)\)
A. N(1;3)
B. N(1;-1)
C. N(-1;-1)
D. N(-5;3)
Câu 6: Trong mặt phẳng tọa độ Oxy, cho hai điểm M(2;3) và N(1;-1). Phép tịnh tiến theo véc tơ \(\overrightarrow{v}\) biến điểm M thành điểm N. Khi đó ta có:
A.\(\overrightarrow{v}=\left(3;2\right)\)
B. \(\overrightarrow{v}=\left(-1;-4\right)\)
C. \(\overrightarrow{v}=\left(1;4\right)\)
D. \(\overrightarrow{v}=\left(-3;2\right)\)
Câu 7: Trong mặt phẳng Oxy và đường tròn \(\left(C\right):x^2+y^2-2x+4y-4=0\). Viết phương trình đường tròn (C') là ảnh của (C) qua \(T\overrightarrow{v}\)
A. \(\left(x-4\right)^2+\left(y-1\right)^2=4\)
B. \(\left(x+4\right)^2+\left(y+1\right)=9\)
C. \(\left(x-4\right)^2+\left(y-1\right)^2=9\)
D. \(x^2+y^2+8x+2y-4=0\)
Câu 8: Trong mặt phẳng tọa độ, xác định của đường thẳng \(\left(d\right):x+y-2=0\) qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}=\left(-3;0\right)\)
A. x+y+3=0
B. x-y-2=0
C. x+y+2=0
D. x+y+1=0