Cho 5 đường thẳng đôi một cắt nhau gọi số giao điểm là m
Tính giá trị nhỏ nhất của m. Tính giá trị lớn nhất của m
Những câu hỏi liên quan
Cho điểm M và năm đường thẳng a, b, c, d, e. Gọi x là số đường thẳng đã cho đi qua điểm M. Tìm giá trị nhỏ nhất và giá trị lớn nhất của x.
Cho điểm M và 4 đường thẳng a,b,c,d. Gọi n là số đường thẳng đã cho đi qua M.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của n.(Vẽ hình trong mỗi trường hợp )
+ Lớn nhất :
Vì M là điểm nên điểm M là giao điểm của các đoạn thẳng nên n = 1
Vậy .....
+Nhỏ nhất
Để n nhỏ nhất thì n = 0 khi và chỉ khi số đường thằng đã cho không đi qua M ( vì đề bài đâu yêu cầu n thuộc N* )
Suy ra n = 0
Vậy ...........
Đúng 0
Bình luận (0)
Cho hàm số
y
x
+
1
x
-
1
. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m A. -6 B.
2
3
C.
3
2
D.
6
5
Đọc tiếp
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
A. -6
B. 2 3
C. 3 2
D. 6 5
Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y' = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3:
Đúng 0
Bình luận (0)
Cho hàm số
y
x
+
1
x
-
1
. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M+m A. -6 B.
2
3
C.
3
2
D.
6
5
Đọc tiếp
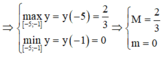
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M+m
A. -6
B. 2 3
C. 3 2
D. 6 5
cho đường thẳng (d) có phương trình y = (2m - 1)x + m + 1 và đường thẳng (d') có phương trình y = x+ 3
a, tính giá trị của m để đường thẳng (d) cắt đường thẳng (d') tại một điểm trên trục tung
b, tìm m để khoản cách từ gốc tọa độ O đến dường thẳng (d) đạt giá trị lớn nhất và giá trị lớn nhất đó bằng nhau
Cho số phức z thỏa mãn
z
-
2
+
z
+
2
5
. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
z
. Tính M + m ? A. M +m
17
2
B. M +m 8 C. M +m 1 D. M +m 4
Đọc tiếp
Cho số phức z thỏa mãn z - 2 + z + 2 = 5 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của z . Tính M + m ?
A. M +m = 17 2
B. M +m = 8
C. M +m = 1
D. M +m = 4
Cho điểm O và 4 đường thẳng a, b, c, d. Gọi m là số đường thẳng đi qua O. Tìm giá trị lớn nhất, giá trị nhỏ nhất của m?
Các bn giúp mk vs mk phải nộp rồi vào ngày mai r nếu ko là mk chết chắc mk sẽ tick cho bn nào nhanh nhất.
Sorry,i can't help you because this years i'm grow up to class 5.
Cho (Cm) là đồ thị của hàm số
y
x
3
+
3
m
x
+
1
(với
m
∈
(
-
∞
;
0
)
là tham số thực). Gọi d là đường thẳng...
Đọc tiếp
Cho (Cm) là đồ thị của hàm số y = x 3 + 3 m x + 1 (với m ∈ ( - ∞ ; 0 ) là tham số thực). Gọi d là đường thẳng đi qua hai điểm cực trị của (Cm). Tìm số các giá trị của m để đường thẳng d cắt đường tròn tâm I(1;0) bán kính R=3 tại hai điểm phân biệt A, Bsao cho diện tích tam giác IAB đạt giá trị lớn nhất.
A.3
B.0
C.1
D.2
Chọn C
.
Vì 
nên phương trình 
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị 
.
Giả sử hàm số có hai điểm cực trị lần lượt là 
và 
, với 
, 
là nghiệm của phương trình 
.
Thực hiện phép chia 
cho 
ta được : 
.
Khi đó ta có: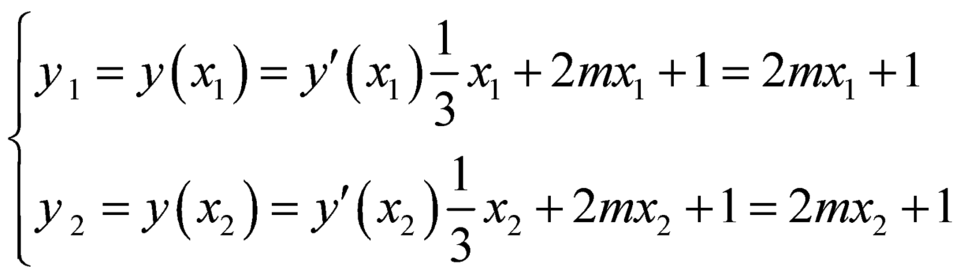 
.
Ta thấy, toạ độ hai điểm 
và 
thoả mãn phương trình 
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là 
.
Ta thấy 
luôn qua 
.
Đặt 
.
.
Xét hàm số 
, 
.
, 
.
Suy ra hàm số 
liên tục và đồng biến trên 
.
Do đó 
.
Vậy 
đạt giá trị lớn nhất 
.
Đúng 0
Bình luận (0)
Cho điểm A và 4 đường thẳng m , n, p ,q.Gọi x là số đường thẳng đã cho đi qua A
Tìm giá trị lớn nhất , giá trị nhỏ nhất của x .
