Cho tam giác ABC . I là một điểm nằm trong tam giác . Chứng minh
IA + IB < CA + CB
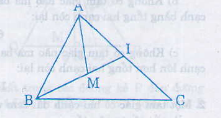
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.
So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.
Ba điểm B, I, C không thẳng hàng.
Xét bất đẳng thức tam giác trong ΔIBC:
IB < IC + CB
⇒ IB + IA < IA + IC + BC (cộng cả hai vế với IA)
hay IB + IA < CA + CB (vì IA + IC = AC)
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạn AC
a) So sánh IB với MI + IA, từ đó chứng minh MA + MB < IB +IA
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB
c) Chứng minh bất đẳng thức MA + MB < CA + CB
a) M nằm trong tam giác nên ABM
=> A, M, I không thẳng hang
Theo bất đẳng thức tam giác với ∆AMI:
AM < MI + IA (1)
Cộng vào hai vế của (1) với MB ta được:
AM + MB < MB + MI + IA
Mà MB + MI = IB
=> AM + MB < BI + IA
b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)
cộng vào hai vế của (2) với IA ta được:
BI + IA < IA + IC + BC
Mà IA + IC = AC
Hay BI + IA < AC + BC
c) Vì AM + MB < BI + IA
BI + IA < AC + BC
Nên MA + MB < CA + CB
Vậy số đo cạnh thứ ba là 11cm
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC
a. So sánh MA với MI +IA; từ đó chứng minhMA+MB<IB+IA
B. So sánh IB với IC+CB, từ đó chứng minh IB+IA<CA+CB
C. Chứng minh bất đẳng thức MA+MB<CA+CB
Bài 1: cho tam giác ABC, điểm K là một điểm nằm trong tam giác. Gọi I là giao điểm của cạnh BK và AC
a, So sánh KA và KI+IA từ đó chứng minh KA + KB< IB+ IA
b, So sánh IB với IC + CB từ đó chứng minh IB + IA < CA + CB
c, Chứng minh bất đẳng thức KA+ KB < CA+CB
.Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC
a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB
c) Chứng minh bất đẳng thức MA + MB < CA + CB
a) M nằm trong tam giác nên ABM
=> A, M, I không thẳng hang
Theo bất đẳng thức tam giác với ∆AMI:
AM < MI + IA (1)
Cộng vào hai vế của (1) với MB ta được:
AM + MB < MB + MI + IA
Mà MB + MI = IB
=> AM + MB < BI + IA
b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)
cộng vào hai vế của (2) với IA ta được:
BI + IA < IA + IC + BC
Mà IA + IC = AC
Hay BI + IA < AC + BC
c) Vì AM + MB < BI + IA
BI + IA < AC + BC
Nên MA + MB < CA + CB
M nằm trong tam giác nên ABM
=> A, M, I không thẳng hang
Theo bất đẳng thức tam giác với ∆AMI:
AM < MI + IA (1)
Cộng vào hai vế của (1) với MB ta được:
AM + MB < MB + MI + IA
Mà MB + MI = IB
=> AM + MB < BI + IA
b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)
cộng vào hai vế của (2) với IA ta được:
BI + IA < IA + IC + BC
Mà IA + IC = AC
Hay BI + IA < AC + BC
c) Vì AM + MB < BI + IA
BI + IA < AC + BC
Nên MA + MB < CA + CB
Vậy số đo cạnh thứ ba là 11cm
)tam giác IMA có:MA<IA+IM(theo bất đẳng thức tam giác)
Cộng MB vào 2 vế trên ta có:
MB+MA<MB+MI+MA
==> MB+MA< IB +IA(1)
b)tam giác ICB có:
IB<BC+IC
Cộng thêm IM vào bất đẳng thức trên ta được:
IB+IA<IA+IC+CB
==>IB+IA< CA +CB(2)
Từ (1) và (2) ta ==>MB+MA<CA+CB
2)
a)ta có: 7 >5==>AC>AB==>góc ABC>ACB
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC
a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB
c) Chứng minh bất đẳng thức MA + MB < CA + CB
bạn này tự hỏi rồi tự trả lời để người khác dung cho a
a) M nằm trong tam giác nên ABM
=> A, M, I không thẳng hàng
Theo bất đẳng thức tam giác với ∆AMI:
AM < MI + IA (1)
Cộng vào hai vế của (1) với MB ta được:
AM + MB < MB + MI + IA
Mà MB + MI = IB
=> AM + MB < BI + IA
b) Ba điểm B, I, C không thẳng hàng nên BI < IC + BC (2)
cộng vào hai vế của (2) với IA ta được:
BI + IA < IA + IC + BC
Mà IA + IC = AC
Hay BI + IA < AC + BC
c) Vì AM + MB < BI + IA
BI + IA < AC + BC
Nên MA + MB < CA + CB
Vậy số đo cạnh thứ ba là 11cm
17.Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC
a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB
c) Chứng minh bất đẳng thức MA + MB < CA + CB
a+b, Áp dụng bất đẳng thức tam giác, ta được: AM < IM + IA (trong tam giác MAI ) và IB < IC + CB ( trong tam giác BMA)
c, từ câu a và b => câu c được nhá (cái sau ý)
cho tam giác ABC và M là một giao điểm nằm trong tam giác
Gọi I là giao điểm của đường thẳng BM và cạnh AC
a) so sánh MA với MI+IA từ đó chứng minh MA+MB<IB+IA
b) so sánh IB với IC+CB từ đó chứng minh IB+IA <CA+CB
c) chứng minh bất đẳng thức MA+MB<CA+CB
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.
a) so sánh MA với MI+IA, từ đó chứng minh MA+MB<IB+IA
b) so sánh IB với IC+IB, từ đó chứng minh IB+IA<CA+CB
c) chứng minh bất đẳng thức MA+MB<CA+CB