Tìm x
4.32.x-2.9x-54=0
Những câu hỏi liên quan
tim x;y:
x^2.9x-y0=5.(y-1)
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
16
x
-
2
.
12
x
+
m
-
2
.
9
x
0
có nghiệm dương? A. 2. B. 3. C. 4. D. 1.
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 . 9 x = 0 có nghiệm dương?
A. 2.
B. 3.
C. 4.
D. 1.
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x − 2.12 x + m − 2 .9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Đáp án B.
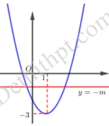
Ta có P T ⇔ 4 3 2 x − 2 4 3 x + m − 2 = 0.
Đặt t = 4 3 x > 0 ⇒ t 2 − 2 t + m − 2 = 0 ⇔ t 2 − 2 t − 2 = − m
Dựa vào đồ thị ta thấy PT có nghiệm lớn hơn 1 ⇔ − m > − 3 ⇔ m < 3
Vậy có 2 giá trị nguyên của m là m = 1 ; m = 2 thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
16
x
-
2
.
12
x
+
m
-
2
.
9
x
0
có nghiệm dương? A. 1. B. 2. C. 4. D. 3.
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 . 9 x = 0 có nghiệm dương?
A. 1.
B. 2.
C. 4.
D. 3.
3.2x+(-1.2)*x+2.7=-4.9
-5.6x+2.9x-3.86=-9.8
\(3.2\times x\left(-1.2\right)\times x+2.7=-4.9\) câu a nhé
\(-5.6\times x+2.9\times x-3.86=-9.8\) câu b nhé
cảm ơn các bạn nhìu
Đúng 0
Bình luận (0)
3.2x+(-1.2)*x+2.7=-4.9
(3.2+(-1.2)*x=-4.9-2.7
2*x=-76
x=-76/2
x=-38
Đúng 0
Bình luận (0)
-5.6*x+2.9*x-3.86=-9.8
(-5.6+2.9)*x=-9.8+3.86
-27*x=-5.94
x=-5.94/-27
x=0.22
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tổng tất cả các nghiệm thực của phương trình
log
6
3
.
4
x
+
2
.
9
x
x
+
1
bằng A. 4 B. 1 C. 0 D. 3
Đọc tiếp
Tổng tất cả các nghiệm thực của phương trình log 6 3 . 4 x + 2 . 9 x = x + 1 bằng
A. 4
B. 1
C. 0
D. 3
3^2x-1+2.9x-1=405
3/5.(3x^3-8/9)-1/2.(3/2-1)=-1/4
\(\left(\dfrac{1}{3}\right)^{x-1}+5.\left(\dfrac{1}{3}\right)^{x+1}=\dfrac{14}{9^3}\)
tìm x ( giúp với mình cần gấp )
Tổng tất cả các nghiệm thực của phương trình
log
6
(
3
.
4
x
+
2
.
9
x
)
x
+
1
bằng A. 4 B. 1 C. 0 D. 3
Đọc tiếp
Tổng tất cả các nghiệm thực của phương trình log 6 ( 3 . 4 x + 2 . 9 x ) = x + 1 bằng
A. 4
B. 1
C. 0
D. 3
cho x-y=7 tính
A=x^2.9x+2)+y(y-2) +2xy +37
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
2
.
9
x
-
3
.
6
x
6
x
-
4
x
≤
2
x
∈...
Đọc tiếp
Tập nghiệm của bất phương trình 2 . 9 x - 3 . 6 x 6 x - 4 x ≤ 2 x ∈ R là ( - ∞ ; a ] ∪ ( b ; c ] . Khi đó a+b+c bằng
A. 3
B. 1
C. 2
D. 0
