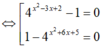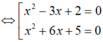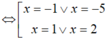Tìm nghiệm nguyên của phương trình: 4x2+ 5y2 = 2022

Những câu hỏi liên quan
Tìm nghiệm nguyên của phương trình :4x^2 -7y^2 =2022
Tìm nghiệm nguyên của phương trình: 3x2 + 13xy + 26(x − y) + 39y2 = 2022
tìm nghiệm nguyên của phương trình \(4x^2-7y^2=2022\)
Tìm tất cả các nghiệm của phương trình
4
x
2
-
3
x
+
2
+
4
x
2
+
6
x
+
5
4
2...
Đọc tiếp
Tìm tất cả các nghiệm của phương trình 4 x 2 - 3 x + 2 + 4 x 2 + 6 x + 5 = 4 2 x 2 + 3 x + 7 + 1
A. x ∈ - 5 ; - 1 ; 1 ; 2
B. x ∈ - 5 ; - 1 ; 1 ; 3
C. x ∈ - 5 ; - 1 ; 1 ; - 2
D. x ∈ 5 ; - 1 ; 1 ; 2
Không dùng công thức nghiệm, tìm số nghiệm của phương trình − 4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Ta có: −4x2 + 9 = 0 ⇔ 4x2 = 9
⇔ x 2 = 9 4 ⇔ x = 3 2 x = − 3 2
phương trình có hai nghiệm
x = 3 2 ; x = − 3 2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Không dùng công thức nghiệm, tìm số nghiệm của phương trình - 4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Đáp án D
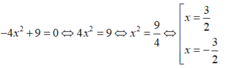
Nên số nghiệm của phương trình là 2.
Đúng 0
Bình luận (0)
Tìm số nghiệm của phương trình sau 2 x − 3 = 4 x 2 − 15
A. 1 nghiệm duy nhất
B. vô nghiệm
C. 3 nghiệm
D. 5 nghiệm
ĐKXĐ: 2 x − 3 ≥ 0 4 x 2 − 15 ≥ 0 ( * )
Với điều kiện (*) phương trình tương đương với
( 2 x − 3 ) 2 = ( 4 x 2 − 15 ) 2 ⇔ 2 x − 3 = 4 x 2 − 15
⇔ 4 x 2 − 2 x − 12 = 0 ⇔ x = 2 x = − 3 2
Thay vào điều kiện (*) ta thấy chỉ có x = 2 thỏa mãn
Vậy phương trình có nghiệm duy nhất x = 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Tìm số nghiệm thực của phương trình
log
2
2
x
2
-
log
4
4
x
2
-
5
0
A. 2 B. 4 C. 1 D. 3
Đọc tiếp
Tìm số nghiệm thực của phương trình log 2 2 x 2 - log 4 4 x 2 - 5 = 0
A. 2
B. 4
C. 1
D. 3
tìm cặp nghiệm nguyên dương của phương trình
x2y2+4=4x2+y2+3x+3y
+4xy vào mỗi vế
=> nhóm VP = (xy+2)^2; VT = (2x+y)^2 + 3x + 3y
=> VT là SCP
kẹp:
(2x+y)^2< (2x+y)^2 + 3x + 3y<(2x+y+2)^2(do x,y nguyên dương)
=> (2x+y)^2 + 3x + 3y = (2x+y+1)^2
=> y = x+1
thay vào
x2y2+4=4x2+y2+3x+3y
r giải pt có x,ytự làm nốt
Đúng 0
Bình luận (3)