(\(\overline{z} \)+2i)(z-4) là số thuần ảo. Trên mặt phẳng tọạ độ,tập hợp điểm biểu diễn số phức w=(1+i)z+1-2i là đường tròn có bán kính bằng.
Xét các số phức z thỏa mãn ( z ¯ +i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 1
B. 5 4
C. 5 2
D. 3 2
Xét các điểm số phức z thỏa mãn z ¯ + i z + 2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng:
A. 1.
B. 5 4
C. 5 2
D. 3 2
Xét các số phức z thoả mãn z ¯ - 2 i z + 3 là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 13
B. 11
C. 11 2
D. 13 2
Xét các số phức z thỏa mãn z ¯ - 2 i z + 2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng?
A. 2 2
B. 2
C. 2
D. 4
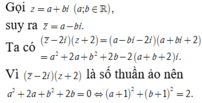
Vậy tập hợp tất cả các điểm biễu diễn số phức z là một đường tròn có bán kính bằng 2 . Chọn B.
Xét các số phức z thoả mãn z ¯ + 2 i z + 3 là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A . 13
B . 11
C. 11 2
D. 13 2
Cho số phức z thỏa mãn |z|=1. Biết tập hợp các điểm biểu diễn số phức w = (3 - 4i)z -1 + 2i là đường tròn tâm I, bán kính R. Tìm tọa độ tâm I và bán kính R của đường tròn đó.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn |z|=1. Biết tập hợp các điểm biểu diễn số phức w=(3-4i)z-1+2i là đường tròn tâm I, bán kính R. Tìm tọa độ tâm I và bán kính R của đường tròn đó
A. I(1;2); R= 5
B. I(1;-2); R=5
C. I(1;2); R=5
D. I(-1;2); R=5
Trong mặt phẳng tọa độ Oxy, cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tập hợp các điểm biểu diễn cho số phức w=z(1+i) là đường tròn
A. Tâm I(3;-1); R = 3 2
B. Tâm I(3;-1);R=3
C. Tâm I(-3;1); R = 3 2
D. Tâm I(3;-1);R=3
Xét các số phức z=x+yi x , y ∈ R có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình (C): x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
![]()
![]()
![]()
![]()