Câu 30: Cho ΔABC = ΔDEF, biết 0 A 50 = , 0 B 65 = . Hỏi ΔDEF là tam giác gì ?
Những câu hỏi liên quan
Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4:5:6 . Cho biết
Δ
D
EF
∽
Δ
A
B
C
và cạnh nhỏ nhất của
Δ
D
E
F
l
à
0
,
8
m
, hãy tính các cạnh còn lại của
Δ
D
E
F
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4:5:6 . Cho biết Δ D EF ∽ Δ A B C và cạnh nhỏ nhất của Δ D E F l à 0 , 8 m , hãy tính các cạnh còn lại của Δ D E F
Vì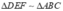 
nên 
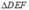cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
Giả sử DE < EF < FD Þ DE = 0,8m.
Ta có
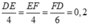
Từ đó tính được EF = 1m và FD = 1,2m
Đúng 0
Bình luận (0)
Hãy chọn câu đúng. Hai ΔABC và ΔDEF có
A
^
80
∘
,
B
^
70
∘
,
F
^
30
∘
; BC 6cm. Nếu ΔABC đồng dạng với ΔDEF thì: A.
D
^
170
∘...
Đọc tiếp
Hãy chọn câu đúng. Hai ΔABC và ΔDEF có A ^ = 80 ∘ , B ^ = 70 ∘ , F ^ = 30 ∘ ; BC = 6cm. Nếu ΔABC đồng dạng với ΔDEF thì:
A. D ^ = 170 ∘ ; EF = 6cm
B. E ^ = 80 ∘ ; ED = 6cm
C. D ^ = 70 ∘
D. C ^ = 30 ∘
Vì tam giác ABC đồng dạng với tam giác DEF nên A ^ = D ^ = 80 ∘ , B ^ = E ^ = 70 ∘ , C ^ = F ^ = 30 ∘
Vậy C ^ = 30 ∘ là đúng
Đáp án: D
Đúng 0
Bình luận (0)
Cho Δ A B C = Δ D E F . Biết rằng AB=5cm; AC=12cm, EF=13cm. Tính chu vi tam giác DEF là
A. 30cm
B. 22 cm
C. 18 cm
D. 20 cm
Cho Δ A B C = Δ D E F . Biết rằng AB=6cm; AC=8cm, EF=10cm. Tính chu vi tam giác DEF là
A. 24cm
B. 20cm
C. 18 cm
D. 30 cm
Cho ΔABC=ΔDEF. Biết ∠A =55o;∠E =75o. Tính các góc còn lại của mỗi tam giác.
Vì ΔABC=ΔDEF nên :∠ A =∠D ; ∠B =∠E ;∠ C = ∠F
Mà ∠A =55o;∠E =75 suy ra: ∠D =55o;∠B =75º
Trong ΔABC, ta có:∠ A +∠B +∠C =180o(tổng ba góc trong tam giac)
Suy ra : ∠C =180o-(∠A +∠B )=180o-(55o+75o)=50o
Mà ∠C = ∠F nên ∠ F =50o
Đúng 0
Bình luận (0)
19 tháng 11 2021 lúc 15:39
Cho ΔABC = ΔDEF. Biết A = \(55^o\), E = \(75^o\).
Tính các góc còn lại của tam giác
\(\Delta ABC=\Delta DEF\Rightarrow\left\{{}\begin{matrix}\widehat{D}=\widehat{A}=55^0\\\widehat{B}=\widehat{E}=75^0\end{matrix}\right.\)
Do tổng 3 góc trong 1 tam giác bằng 180 độ:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow55^0+75^0+\widehat{C}=180^0\)
\(\Rightarrow\widehat{C}=50^0\)
\(\Rightarrow\widehat{F}=\widehat{C}=50^0\)
Đúng 1
Bình luận (1)
cho ΔABC =ΔDEF. Tính chu vi mỗi tam giác, biết rằng AB=5cm, BC=7cm, DF=6cm
Vì ΔABC = ΔDEF (gt)
=> AC = DF = 6cm
Chu vi ΔABC là: AB + BC + AC = 5 + 7 + 6 = 18(cm)
Lại có: ΔABC = ΔDEF(gt)
=> chu vi ΔABC = chu vi ΔDEF = 18cm
Vậy chu vi ΔABC : 18cm
chu vi ΔDEF: 18cm
Đúng 1
Bình luận (0)
Cho ΔABC = ΔDEF. Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi mỗi tam giác là tổng độ dài ba cạnh của tam giác đó).
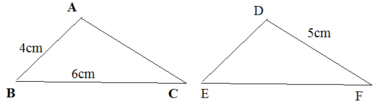
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Đúng 0
Bình luận (0)
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...b) Nếu
Δ
A
B
C
~
Δ
D
E
F
với tỉ số đồng dạng là 1/2 và
Δ
D
E
F
~
Δ
M
N
P
với tỉ số đồng dạng là 4/3 thì
Δ
M
N
P...
Đọc tiếp
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu Δ A B C ~ Δ D E F với tỉ số đồng dạng là 1/2 và Δ D E F ~ Δ M N P với tỉ số đồng dạng là 4/3 thì Δ M N P ~ Δ A B C với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho A I / A B = A K / B C t h ì I K / / B C . . . .
d) Hai tam giác đồng dạng thì bằng nhau....