viết phương trình mặt cầu S qua ba điểm A(2;0;1), B(1;3;2), C(3;2;0) có tâm nằm trong mặt phẳng xOy
AI GIẢI TRÌNH BÀYCHI TIẾT VÀ LÀM XONG TRƯỚC SẼ ĐƯỢC TICK NHIỀU NHÉ
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P): x+y-2z+4=0
![]()
![]()
![]()
![]()
Cho ba điểm A(3;1;1), B(0;1;4), C(-1;-3;1). Viết phương trình mặt cầu (S) đi qua A, B, C và có tâm nằm trên mặt phẳng (P):x+y-2z+4=0
A. x + 1 2 + y - 1 2 + z + 2 2 = 9
B. x - 1 2 + y + 1 2 + z - 2 2 = 3
C. x - 1 2 + y + 1 2 + z - 2 2 = 9
D. x + 1 2 + y - 1 2 + z + 2 2 = 3
Chọn C
Gọi tâm mặt cầu I(x;-x+2z-4;z). Tìm x,z từ hệ hai phương trình IA=IB=IC
Viết phương trình mặt cầu (S) đi qua điểm A(5;-2;1) và có tâm C(3;-3;1)
A. x + 3 2 + y - 3 2 + z + 1 2 = 5
B. x - 3 2 + y + 3 2 + z + 1 2 = 5
C. x - 3 2 + y + 3 2 + z - 1 2 = 5
D. x - 3 2 + y + 3 2 + z - 1 2 = 5
Viết phương trình mặt cầu (S) biết (S) qua bốn điểm A ( 1 ; 2 ; - 4 ) ; B ( 1 ; - 3 ; 1 ) ; C ( 2 ; 2 ; 3 ) v à D ( 1 ; 0 ; 4 ) .
A. x + 2 2 + y - 1 2 + z 2 = 26
B. x - 2 2 + y + 1 2 + z 2 = 13
C. x + 2 2 + y + 1 2 + z 2 = 52
D. Đáp án khác
Chọn A.
Gọi phương trình mặt cầu (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0, (a2 + b2 + c2 - d > 0)
có tâm I (a;b;c) và bán kính ![]()
Do A(1;2;-4) ∈ (S)nên: 12 + 22 + (-42 – 2.a.1 – 2b .2 - 2c.(-4) + d = 0 hay -2a - 4b + 8c + d = -21 (1)
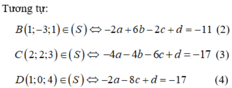
Giải hệ (1), (2), (3), (4) ta có: a = -2; b = 1; c = 0; d = -21, suy ra phương trình mặt cầu (S) :
(x + 2)2 + (y - 1)2 + z2 = 26.
Viết phương trình mặt cầu (S) biết (S) qua bốn điểm A ( 1 ; 2 ; - 4 ) ; B ( 1 ; - 3 ; 1 ) ; C ( 2 ; 2 ; 3 ) v à D ( 1 ; 0 ; 4 ) .
A. x + 2 2 + y - 1 2 + z 2 = 26
B. x - 2 2 + y + 1 2 + z 2 = 13
C. x + 2 2 + y + 1 2 + z 2 = 52
D. Đáp án khác
Chọn A.
Gọi phương trình mặt cầu (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0, (a2 + b2 + c2 - d > 0)
có tâm I (a;b;c) và bán kính ![]()
Do A(1;2;-4) ∈ (S)nên: 12 + 22 + (-42 – 2.a.1 – 2b .2 - 2c.(-4) + d = 0 hay -2a - 4b + 8c + d = -21 (1)
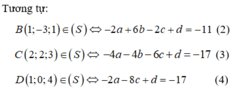
Giải hệ (1), (2), (3), (4) ta có: a = -2; b = 1; c = 0; d = -21, suy ra phương trình mặt cầu (S) :
(x + 2)2 + (y - 1)2 + z2 = 26.
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + ( z - 1 ) 2 = 4 và điểm A ( 2 ; 2 ; 1 ) . Từ điểm A kẻ ba tiếp tuyến AB, AC, AD với B, C, D là các tiếp điểm. Viết phương trình mặt phẳng ( B C D ) .
A . 2 x + 2 y + z - 1 = 0 .
B . 2 x + 2 y + z + 1 = 0 .
C . 2 x + 2 y + z - 3 = 0 .
D . 2 x + 2 y + z - 5 = 0 .
Trong không gian Oxyz, cho điểm \(D\left(-3;1;2\right)\) và mặt phẳng \(\left(\alpha\right)\) đi qua ba điểm \(A\left(1;0;11\right),B\left(0;1;10\right),C\left(1;1;8\right)\)
a) Viết phương trình đường thẳng AC
b) Viết phương trình tổng quát của mặt phẳng \(\left(\alpha\right)\)
c) Viết phương trình mặt cầu (S) tâm D, bán kính r = 5. Chứng minh mặt phẳng \(\left(\alpha\right)\) cắt mặt cầu (S)
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + ( z - 1 ) 2 = 4 và điểm A(2;2;1). Từ điểm A kẻ ba tiếp tuyến AB, AC, AD với B, C, D là các tiếp điểm. Viết phương trình mặt phẳng (BCD).
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng (P) đi qua ba điểm A ( 3 2 ; 0 ; 0 ) , B ( 0 ; 3 2 ; 0 ) , C ( 0 ; 0 ; - 3 ) , và mặt cầu (S): ( x - 3 ) 2 + ( y - 2 ) 2 + ( z - 5 ) 2 = 36 . Gọi ∆ là đường thẳng đi qua điểm E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình ∆ là
A. x = 2 + 9 t y = 1 + 9 t z = 3 + 8 t
B. x = 2 - 5 t y = 1 + 3 t z = 3
C. x = 2 + t y = 1 - t z = 3
D. x = 2 + 4 t y = 1 + 3 t z = 3 - 3 t