cho (P):y=X2
TÌM trên (p) 2 điểm A,B sao cho tam giác OAB đều
CHo parabol y= 1/2x^2 tìm trên (p) hai điểm A,B sao cho tam giác OAB đều
Cho tam giác OAB đều. Trên tia đối OA,OB lấy theo thứ tự 2 điểm C và D sao cho OC=OD. Từ B và C kẻ BM vuông góc AC, CN vuông góc BD. Gọi P là trung điểm BC. Cm: Tam giác MNP đều
Tam giác MBC vuông tại M và có MP là trung tuyến => MP = 1/2 BC
Tam giác NBC vuông tại N và có NP là trung tuyến => NP = 1/2 BC
Tam giác OAD có MN là đường trung bình => MN = 1/2 AD
Tam giác OAD = tam giác OBC (trường hợp C-G-C) => AD = BC
Vậy MN = 1/2 AD = 1/2 BC
=> MP = NP = MN (vì đều = 1/2 BC)
=> Tam giác MNP đều
Cho Tam giác đều OAB . Trên tia đối của các tia OA vàOB lấy theo thứ tự hai điểm C và D sao cho ÓC = OD . Từ B và C kẻ BM Vuông góc vớiAC , CN vuông góc với BC chứng minh rằng
a, Tam giác COD đều
b, AD=BC
c, Tam giác MNP đều
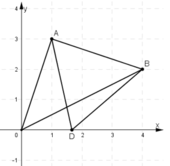
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
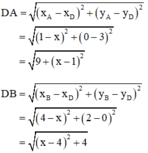
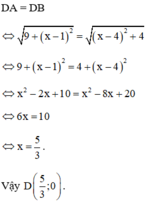
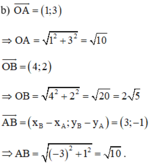
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
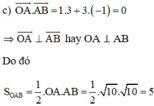
trong tọa độ Oxy, cho đường tròn C: (x-2)2+(y+10)2=16 điểm A di động trên (C). Dựng tam giác OAB sao cho OA=2OB và góc lượng giác (OA,OB)=90. ĐIểm A di động trên (C) thì điểm B là đường tròn nào?
Trên mặt phẳng tọa độ Oxy cho hai điểm \(A\left(1;3\right);B\left(4;2\right)\)
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB
b) Tính chu vi tam giác OAB
c) Tính diện tích tam giác OAB
Hãy vẽ 2 tam giác đều phân biệt OAB, OAF có cạnh OA = 2(cm). Kéo dài đoạn thẳng AO, BO, FO về phía O rồi lấy lần lượt trên những phần kéo dài đó các điểm D, E, C sao cho OD=OE=OC=2(cm)
a) Hỏi ABCDEF là hình gì?
b) Trên hình lục giác đều ABCDEF, tam giác ACE có phải là tam giác đều k?
Cho ∠xOy = 90◦. a) Dựng tia Oz nằm giữa hai tia Ox, Oy sao cho ∠xOz = 30◦. b) Trên tia Ox,Oz lần lượt lấy các điểm A,B sao cho OA = OB (A,B ̸= O). Dựng về phía bên trong tam giác OAB tam giác đều ABC. Đường thẳng AC cắt Oy tại D. Chứng minh rằng C là trung điểm của AD. c) Chứng minh rằng đường trung trực của các đoạn thẳng CO,CB và tia Oy đồng quy. Giúp nình vơi!!
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC. Trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Chứng minh:
a) Tam giác OAB = tam giác ODC.
b) Góc ACD = 90 độ.
c) BC = 2 OA.
XÉT\(\Delta OAB\)VÀ\(\Delta ODC\)
AO=OD
BO=OC =>\(\Delta OAB=\Delta ODC\left(c-g-c\right)\)
^AOB=^COD
=>^B=^BCD
TA LẠI CÓ ^B + ^ACB=\(90^0\)
=>^BCD + ^ACB=\(90^0\)
XÉT \(\Delta ACP\)VÀ\(\Delta CAB\)
^BAC=^ACD=\(90^0\)
AB=CD =>\(\Delta ACP=\Delta CAB\)(2 CẠNH GÓC VUÔNG)
AC chung
=>BC=AP
vì \(AO=OD=\frac{AD}{2}\)nên \(AO=\frac{BC}{2}\) hay BC=2AO
mk sẽ tích và add cho bạn nào làm đúng và nhanh nhất trong hôm nay thôi nha vì mk đang cần gấp cho ngày mai.