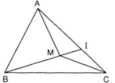
Theo giả thiết, điểm M nằm trong tam giác ABC nên điểm M không nằm trên cạnh AC.

⇒ A, M, I không thẳng hàng.

Xét bất đẳng thức tam giác trong ΔAMI:

MA < MI + IA

⇒ MA + MB < MB + MI + IA (cộng cả hai vế với MB)

hay MA + MB < IB + IA (vì MB + MI = IB).

tự vẽ hình

a) xét tam giác MIA có: MA < MI+IA (bđt tam giác)

                             =>   MA+MB < MI+IA+MB

                              => MA+MB < (MI+MB)+IA 

                             => MA+MB < IB+IA (1)

 b) xét tam giác BIC có: IB < IC+CB (bđt tam giác)

                               => IB+IA < IC+CB+IA

                              => IB+IA < (IC+IA)+CB

                              => IB+IA < CA+CB  (2)

c) từ (1) và (2) => MA+MB < CA+CB

a)  M nằm trong tam giác nên ABM

=> A, M, I không thẳng hang

Theo bất đẳng thức tam giác với ∆AMI:

AM < MI + IA (1)

Cộng vào hai vế của (1) với MB ta được:

AM + MB < MB + MI + IA

Mà MB + MI = IB

=> AM + MB < BI + IA

b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)

cộng vào hai vế của (2) với IA ta được:

BI + IA < IA + IC + BC

Mà IA + IC = AC

Hay BI + IA < AC + BC

c) Vì AM + MB < BI + IA

       BI + IA < AC + BC

Nên MA + MB < CA + CB

M nằm trong tam giác nên ABM

=> A, M, I không thẳng hang

Theo bất đẳng thức tam giác với ∆AMI:

AM < MI + IA (1)

Cộng vào hai vế của (1) với MB ta được:

AM + MB < MB + MI + IA

Mà MB + MI = IB

=> AM + MB < BI + IA

b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)

cộng vào hai vế của (2) với IA ta được:

BI + IA < IA + IC + BC

Mà IA + IC = AC

Hay BI + IA < AC + BC

c) Vì AM + MB < BI + IA

       BI + IA < AC + BC

Nên MA + MB < CA + CB

Vậy số đo cạnh thứ ba là 11cm

)tam giác IMA có:MA<IA+IM(theo bất đẳng thức tam giác)
Cộng MB vào 2 vế trên ta có:
MB+MA<MB+MI+MA
==> MB+MA< IB +IA(1)
b)tam giác ICB có:
IB<BC+IC
Cộng thêm IM vào bất đẳng thức trên ta được:
IB+IA<IA+IC+CB
==>IB+IA< CA +CB(2)
Từ (1) và (2) ta ==>MB+MA<CA+CB
2) 
a)ta có: 7 >5==>AC>AB==>góc ABC>ACB

bạn này tự hỏi rồi tự trả lời để người khác dung cho a

a)  M nằm trong tam giác nên ABM

=> A, M, I không thẳng hàng

Theo bất đẳng thức tam giác với ∆AMI:

AM < MI + IA (1)

Cộng vào hai vế của (1) với MB ta được:

AM + MB < MB + MI + IA

Mà MB + MI = IB

=> AM + MB < BI + IA

b) Ba điểm B, I, C không thẳng hàng nên BI < IC + BC (2)

cộng vào hai vế của (2) với IA ta được:

BI + IA < IA + IC + BC

Mà IA + IC = AC

Hay BI + IA < AC + BC

c) Vì AM + MB < BI + IA

BI + IA < AC + BC

Nên MA + MB < CA + CB

Vậy số đo cạnh thứ ba là 11cm

hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh

a)Tam giác MAI có MA<MI+IA(quan hệ 3 cạnh trong tam giác)

Nên:  có:   MA<MI+IA

          MA+MB<MI+IA+MB

          MA+MB<IA+IB

Vậy          MA+MB<IA+IB (1)

b)Tam giác CBI có IB<IC+CB (quan hệ 3 cạnh trong tam giác)

Nên                     IB<IC+CB

             IB+IA<IC+CB+IA

            IB+IA<CA+CB

Vậy IB+IA<CA+CB (2)

c) Từ (1) và (2) suy ra

MA+MB<CA+CB

ze:13.0pt; mso-fareast-font-family:Calibri; mso-fareast-theme-font:minor-latin; color:#C00000;} .MsoPapDefault {mso-style-type:export-only; margin-bottom:10.0pt; line-height:115%;} @page Section1 {size:8.5in 11.0in; margin:1.0in 1.0in 1.0in 1.0in; mso-header-margin:.5in; mso-footer-margin:.5in; mso-paper-source:0;} div.Section1 {page:Section1;} /* List Definitions */ @list l0 {mso-list-id:1148129261; mso-list-type:hybrid; mso-list-template-ids:-1807209504 -1162451228 67698691 67698693 67698689 67698691 67698693 67698689 67698691 67698693;} @list l0:level1 {mso-level-start-at:2; mso-level-number-format:bullet; mso-level-text:; mso-level-tab-stop:none; mso-level-number-position:left; text-indent:-.25in; font-family:Wingdings; mso-fareast-font-family:Calibri; mso-fareast-theme-font:minor-latin; mso-bidi-font-family:"Times New Roman";} ol {margin-bottom:0in;} ul {margin-bottom:0in;} -->

a)Xét tam giác NMI và Tam giác NHI có

MNI=INH(gt)

NM=NH

NI cạnh chung

Nên tgiac NMI=Tgiac NHI(c-g-c)

b) Xét tgiac MIF và tgiac HIP có

IM=IH(vì tgiac NMI=tgiac NHI)

MIF=HIP(đối đỉnh)

Nên tgiac MIF=Tgiac HIP (ch-gn)

Do đó IF=IP( 2 cạnh tương ứng)

Vậy Tam giác IFP cân tại I

c) Tam giác IHP: có IHP=90 nên IP>IH(tính chất cạnh đối diện góc lớn nhất)

Mà  IP=IF => IF>IH

Vậy IF>IH

câu dưới mình bị nhầm á thông cảm hen

a) M nằm trong tam giác nên ABM

=> A, M, I không thẳng hang

Theo bất đẳng thức tam giác với ∆AMI:

AM < MI + IA (1)

Cộng vào hai vế của (1) với MB ta được:

AM + MB < MB + MI + IA

Mà MB + MI = IB

=> AM + MB < BI + IA

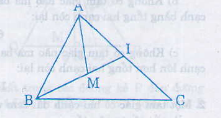
b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)

cộng vào hai vế của (2) với IA ta được:

BI + IA < IA + IC + BC

Mà IA + IC = AC

Hay BI + IA < AC + BC

c) Vì AM + MB < BI + IA

BI + IA < AC + BC

Nên MA + MB < CA + CB

Vậy số đo cạnh thứ ba là 11cm

a+b, Áp dụng bất đẳng thức tam giác, ta được: AM < IM + IA (trong tam giác MAI ) và IB < IC + CB ( trong tam giác BMA)

c, từ câu a và b => câu c được nhá (cái sau ý)