cho tam giác mqn. Từ điểm H thuộc cạnh qn kẻ các đường thẳng song song với cạnh qm và cạnh nm, chúng cách các cạnh qm và mn tại f và c. Chứng minh rằng MC/MQ+MF/MN=1

Những câu hỏi liên quan
Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E. Chứng minh rằng: A E A B + A F A C = 1
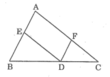
Trong tam giác ABC ta có: DE // AC (gt)
Suy ra: 
Lại có: DF // AB (gt)
Suy ra: 
Cộng từng vế (1) và (2) ta có:
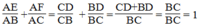
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD.Trên các cạnh AB lấy điểm M bất kì. Từ M kẻ MN song song với AD( N thuộc DC). Gọi H là trung điểm của BM. Đường thẳng qua H vuông góc với BM lần lượt cắt các đường thẳng MN và BC tại E và F. a) Chứng minh các tứ giác AMND; BMNC là hình bình hànhb)Chứng minh E và F đối xứng nhau qua AB từ đó suy ra tứ giác MEBF là hình bình hành. c) Kéo dài MF cắt đường thẳng DC tại I. Chứng minh tứ giác AMID là hình thang cân. Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác...
Đọc tiếp
Cho hình bình hành ABCD.Trên các cạnh AB lấy điểm M bất kì. Từ M kẻ MN song song với AD( N thuộc DC). Gọi H là trung điểm của BM. Đường thẳng qua H vuông góc với BM lần lượt cắt các đường thẳng MN và BC tại E và F. a) Chứng minh các tứ giác AMND; BMNC là hình bình hành
b)Chứng minh E và F đối xứng nhau qua AB từ đó suy ra tứ giác MEBF là hình bình hành.
c) Kéo dài MF cắt đường thẳng DC tại I. Chứng minh tứ giác AMID là hình thang cân.
Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác BCNE là hình thang cân?
Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E. CHứng minh AEDF là HÌnh bình hành
Bài 2: Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E. Chứng minh rằng: AE trên AB+À trên AC =1
giúp mik với mik cần gấp thanks nhiều![]()
Cho tam giác MNP. Từ một điểm Q trên cạnh NP, kẻ các đường song song với cạnh MN, MP lần lượt tại E, F. Chứng minh
a) tam giác ENQ đồng dạng tam giác MNP; tam giác FQP đồng dạng với tam giác MNP
b) ME/MN+MF/MP=1
Cho tam giác ABC cân tại A. Lấy D thuộc cạnh BC. Qua D kẻ các đường thẳng song song với các cạnh bên, chúng cắt AB và AC lần lượt tại F và E. Chứng minh rằng DE + DF = AB
nguồn:https://olm.vn/hoi-dap/detail/327640299239.html


Cho tam giác ABC,từ điểm D trên cạnh BC kẻ các đường thẳng song song với cạnh AB và AC,chúng cắt các cạnh AB và AC theo thứ tự tại E và F. Chứng minh rằng: \(\frac{AF}{AB}\)+\(\frac{AE}{AC}\)= 1
Thấy đề sai sai á :)) Hóng cách làm vậy ....
Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB lần lượt tại F và E. Chứng minh AE\(\frac{AE}{Ab}+\frac{AF}{AC}=1\)
Vì DF//AB (gt) . Áp dụng định lý Talet ta có : \(\frac{AF}{AC}=\frac{BD}{BC}\)(1)
Vì DE//AC (gt) . Áp dụng định lý Talet ta có : \(\frac{AE}{AB}=\frac{CD}{BC}\)(2)
Từ (1);(2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{BD}{BC}+\frac{CD}{BC}=\frac{BD+CD}{BC}=\frac{BC}{BC}=1\)(Đpcm)
Đúng 0
Bình luận (0)
dcho tam giác ABC cân tại A có cạnh bên bằng k . Trên cạnh đáy BC lấy điểm M tùy ý. Qua M kẻ 2 đường thẳng AB lần lượt song song với các cạnh bên. Chúng cắt AB và AC lần lượt theo thứ tự tại E và F .
a) Chứng minh tam giác EBM và tam giác FCM lÀ 2 tam giác cân.
b) Tính ME+MF theo k.
c) Gọi O là trung điểm EF . Chứng minh rằng 3 điểm A, O, M thẳng hàng














