ΔABC nhọn. Dựng ra bên ngoài ΔABC các hình vuông ABDE, ACFG. Kẻ AH vuông góc với BC cắt EG tại K. Trên tia đối tia KH lấy điểm L sao cho KL = KA. CMR các đường thẳng AH, BF và CD đồng quy

Những câu hỏi liên quan
ΔABC nhọn. Dựng ra bên ngoài ΔABC các hình vuông ABDE, ACFG. Kẻ AH vuông góc với BC cắt EG tại K. Trên tia đối tia KH lấy điểm L sao cho KL = KA. CMR các đường thẳng AH, BF và CD đồng quy
ΔABC nhọn. Dựng ra bên ngoài ΔABC các hình vuông ABDE, ACFG. Kẻ AH vuông góc với BC cắt EG tại K. Trên tia đối tia KH lấy điểm L sao cho KL = KA. CMR các đường thẳng AH, BF và CD đồng quy
ΔABC nhọn. Dựng ra bên ngoài ΔABC các hình vuông ABDE, ACFG. Kẻ AH vuông góc với BC cắt EG tại K. Trên tia đối tia KH lấy điểm L sao cho KL = KA. CMR các đường thẳng AH, BF và CD đồng quy
Nói chính xác luôn là tam giác vuông cân, lại bày hình vuông chi
Đúng 0
Bình luận (0)
nếu có ai k mình thì nhớ nhắn tin cho mình biết để mình k lại nha
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, về phía ngoài vẽ các hình vuông: ABDE, ACFG. Gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm A sao cho M là trung điểm của AA.a) Chứng minh AAEGb) AM cắt EG tại N. Chứng minh NA vuông góc với GEc) Từ G và E kẻ các đường thẳng // với AE và AG. Chúng cắt nhau tại I. Vẽ đường cao AH của tam giác ABC.Chứng minh: I,A,H thẳng hàngChứng mminh CIBFd) Chứng minh CD,BF,AH đồng quy
Đọc tiếp
Cho tam giác ABC nhọn, về phía ngoài vẽ các hình vuông: ABDE, ACFG. Gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm A' sao cho M là trung điểm của AA'.
a) Chứng minh AA'=EG
b) AM cắt EG tại N. Chứng minh NA vuông góc với GE
c) Từ G và E kẻ các đường thẳng // với AE và AG. Chúng cắt nhau tại I. Vẽ đường cao AH của tam giác ABC.
Chứng minh: I,A,H thẳng hàng
Chứng mminh CI=BF
d) Chứng minh CD,BF,AH đồng quy
giúp vs, câu a làm rcho tam giác ABC nhọn, về phía ngoài vễ các hình vuông ABDE, ACFG. gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm A sao cho M là trung điểm của AA.a) Cm: AA EG.b) AM cắt GE tại N. Cm: NA vuông góc GE.c) từ G và E kẽ các đường thẳng song song vs AE và AG chúng cắt nhau tại I. vẽ đường cao AH của tam giác ABC. Cm: I, A, H thẳng hàng.d) Cm; CI BF, CI vuông góc BFe) Cm: CD, BF, AH đồng quy
Đọc tiếp
giúp vs, câu a làm r
cho tam giác ABC nhọn, về phía ngoài vễ các hình vuông ABDE, ACFG. gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm A' sao cho M là trung điểm của AA'.
a) Cm: AA' = EG.
b) AM cắt GE tại N. Cm: NA vuông góc GE.
c) từ G và E kẽ các đường thẳng song song vs AE và AG chúng cắt nhau tại I. vẽ đường cao AH của tam giác ABC. Cm: I, A, H thẳng hàng.
d) Cm; CI = BF, CI vuông góc BF
e) Cm: CD, BF, AH đồng quy
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABCa, vẽ điểm H thuộc BC sao cho AH vuông góc với BC; các điểm I và J sao cho EI vuông góc với AH và GJ vuông góc với AH. Chứng minh tam giác ABH tam giác EAI; tam giác ACH tam giác GAJb, gọi AH cắt EG tại K (K là trung điểm của EG tức là AK là trung tuyến tam giác AEG) ; gọi L là điểm thuộc AK sao cho K là trung điểm của AL. Chứng minh ALBCc, chứng minh tam giác ABL tam giác BDC. Từ đó suy ra CD là đường cao tam giác BCLd,chứng minh AH,BF...
Đọc tiếp
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC
a, vẽ điểm H thuộc BC sao cho AH vuông góc với BC; các điểm I và J sao cho EI vuông góc với AH và GJ vuông góc với AH. Chứng minh tam giác ABH= tam giác EAI; tam giác ACH= tam giác GAJ
b, gọi AH cắt EG tại K (K là trung điểm của EG tức là AK là trung tuyến tam giác AEG) ; gọi L là điểm thuộc AK sao cho K là trung điểm của AL. Chứng minh AL=BC
c, chứng minh tam giác ABL= tam giác BDC. Từ đó suy ra CD là đường cao tam giác BCL
d,chứng minh AH,BF,CD đồng quy
giúp với xong trước chiều nay, câu a biết làm rồicho tam giác nhọn ABC, về phía ngoài vẽ các hình vuông ABDE, ACFG. gọi M là trung điểm của BC trên tia đối của tia MA lấy điểm A sao cho M là trung điểm của AA.a) Cm: AA EGb) AM cắt GE tại N. Cm: NA vuông góc GEc) Từ G và E kẽ các đường thẳng song song với AE và AG chúng cắt nhau tại I. Vẽ đường cao Ah của tam giác ABC. Cm: I,A,H thẳng hàngd) Cm: CI BF và CI vuông góc BFe) Cm: CD, BF, AH đồng quy
Đọc tiếp
giúp với xong trước chiều nay, câu a biết làm rồi
cho tam giác nhọn ABC, về phía ngoài vẽ các hình vuông ABDE, ACFG. gọi M là trung điểm của BC trên tia đối của tia MA lấy điểm A' sao cho M là trung điểm của AA'.
a) Cm: AA' = EG
b) AM cắt GE tại N. Cm: NA vuông góc GE
c) Từ G và E kẽ các đường thẳng song song với AE và AG chúng cắt nhau tại I. Vẽ đường cao Ah của tam giác ABC. Cm: I,A,H thẳng hàng
d) Cm: CI = BF và CI vuông góc BF
e) Cm: CD, BF, AH đồng quy
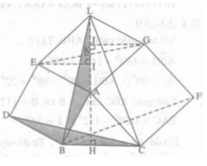
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước. Chứng minh rằng các đường thẳng AH, BF, CD đồng quy.
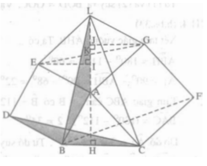
Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.
Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chúng đồng quy.
Đúng 0
Bình luận (0)
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước. Gọi H là điểm thuộc đường thẳng BC sao cho AH ⊥ BC. Gọi I, J là các điểm thuộc đường thẳng AH sao cho EI ⊥ AH và GJ ⊥ AH. Chứng minhΔABH ΔEAI, ΔACH ΔGAJTừ đó suy ra đường thẳng AH cắt EG tại trung điểm K của EG (tức là AK là trung tuyến của tam giác AEG)
Đọc tiếp
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước. Gọi H là điểm thuộc đường thẳng BC sao cho AH ⊥ BC. Gọi I, J là các điểm thuộc đường thẳng AH sao cho EI ⊥ AH và GJ ⊥ AH. Chứng minh
ΔABH = ΔEAI, ΔACH = ΔGAJ
Từ đó suy ra đường thẳng AH cắt EG tại trung điểm K của EG (tức là AK là trung tuyến của tam giác AEG)
+) Xét tam giác EIA vuông tại I nên :
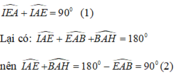
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
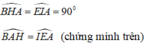
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
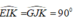
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.
Đúng 0
Bình luận (0)








