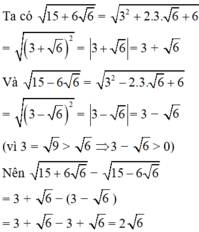\(3\times\dfrac{5}{11}=\dfrac{15}{11}\)

\(\dfrac{16}{64}\times\dfrac{15}{24}=\dfrac{5}{32}\)

\(\dfrac{1}{6}:\dfrac{1}{5}=\dfrac{5}{6}\)

\(\dfrac{7}{12}:\dfrac{1}{4}=\dfrac{7}{3}\)

= 15/11

= 5/32

= 5/6

= 7/3

= 59

= 47/5

= 11/18

= 31/15     nha

Đáp án đúng : A

Đáp án là B

15 - 6 6 + 15 + 6 6

= 9 - 6 6 + 6 + 9 + 6 6 + 6 = 3 - 6 2 + 3 + 6 2

= |3 -  6 | + |3 +  6 |

= 3 - 6 + 3 +  6

= 6

Đáp án là A

\(15.\left(-176\right)+15.76\)

\(=15.76-15.176\)

\(=15.\left(76-176\right)\)

\(=-15.100=-1500\)

 15( - 176) + 15 x 76

= 15[( -176) + 76]

=15(-100)

= -1500

hok good

15.(-176)+15.76

15.[(-176)+76]

15.-100

-1500

\(A=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{66}\)

\(\frac{A}{2}=\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{132}\)

\(\frac{A}{2}=\frac{1}{4\cdot5}+\frac{1}{5\cdot6}+\frac{1}{6\cdot7}+...+\frac{1}{11\cdot12}\)

\(\frac{A}{2}=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{11}-\frac{1}{12}\)

\(\frac{A}{2}=\frac{1}{4}-\frac{1}{12}\)

\(\Rightarrow A=\frac{2}{4}-\frac{2}{12}=\frac{16}{48}\)

\(B=\frac{1}{6}+\frac{1}{10}+\frac{1}{15}+...+\frac{1}{55}\)

\(\frac{B}{2}=\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+...+\frac{1}{110}\)

\(\frac{B}{2}=\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+\frac{1}{5\cdot6}+...+\frac{1}{10\cdot11}\)

\(\frac{B}{2}=\frac{1}{3}-\frac{1}{4}+...+\frac{1}{10}-\frac{1}{11}\)

\(\frac{B}{2}=\frac{1}{3}-\frac{1}{11}\)

\(\Rightarrow B=\frac{2}{3}-\frac{2}{11}=\frac{16}{33}\)

Mà \(\frac{16}{48}< \frac{16}{33}\Rightarrow A< B\)

Vậy : A < B

\(B=\frac{2}{15}+\frac{2}{35}+\frac{2}{63}+...+\frac{2}{399}\)

\(B=\frac{2}{3×5}+\frac{2}{5×7}+\frac{2}{7×9}+...+\frac{2}{19×21}\)

\(B=\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{19}-\frac{1}{21}\)

\(B=\frac{1}{3}-\frac{1}{21}\)

\(B=\frac{2}{7}\)

A=\(\frac{1}{3}\)+\(\frac{1}{6}\)+\(\frac{1}{10}\)+\(\frac{1}{15}\)+...+\(\frac{1}{66}\) 

A=\(\frac{1}{1\cdot3}\) +\(\frac{1}{2\cdot3}\) +\(\frac{1}{2\cdot5}\)+...+\(\frac{1}{6\cdot11}\)

A=\(\frac{1}{1}-\frac{1}{3}+\frac{1}{2}-\frac{1}{3}+\frac{1}{2}-\frac{1}{5}+...+\frac{1}{6}-\frac{1}{11}\)

A=\(\frac{1}{1}-\frac{1}{11}\)

=>A=\(\frac{10}{11}\)

B=\(\frac{2}{15}+\frac{2}{35}+\frac{2}{63}+...+\frac{2}{399}\) 

2B=\(\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\frac{1}{7\cdot9}+...+\frac{1}{19\cdot21}\)

2B=\(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{19}-\frac{1}{21}\)

2B=\(\frac{1}{3}-\frac{1}{21}\)

2B=\(\frac{2}{7}\)

B=\(\frac{2}{7}:2\)

=>B=\(\frac{1}{7}\)