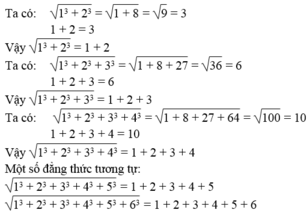Chứng minh rằng: A= 13+23+33+43+...+20163 là số chính phương

Những câu hỏi liên quan
Chứng tỏ rằng, mỗi tổng hoặc hiệu sau đây là một số chính phương:a)
3
2
+
4
2
b)
13
2
-
5
2
c)
1
3
+
2
3
+
3
3
+
4
3
Đọc tiếp
Chứng tỏ rằng, mỗi tổng hoặc hiệu sau đây là một số chính phương:
a) 3 2 + 4 2
b) 13 2 - 5 2
c) 1 3 + 2 3 + 3 3 + 4 3
Chứng tỏ rằng, mỗi tổng hoặc hiệu sau đây là một số chính phương:a,
3
2
+
4
2
b,
13
2
-
5
2
c,
1
3
+...
Đọc tiếp
Chứng tỏ rằng, mỗi tổng hoặc hiệu sau đây là một số chính phương:
a, 3 2 + 4 2
b, 13 2 - 5 2
c, 1 3 + 2 3 + 3 3 + 4 3
a, 3 2 + 4 2 = 25 = 5 2 là số chính phương.
b, 13 2 - 5 2 = 144 = 12 2 là số chính phương.
c, 1 3 + 2 3 + 3 3 + 4 3 = 100 = 10 2 là số chính phương.
Đúng 0
Bình luận (0)
Bài 2: Các số sau có phải là số chính phương không?
1. 13 + 23 ; 13 + 23 + 33 ; 13 + 23 + 33 + 43 ; 13 + 23 + 33 + 43 + 53
2. 1262 + 1 ; 100! + 8 ; 1012 - 3 ; 1010 + 7 ; 11 + 112 + 113
3. 32 + 22 b) 62 + 82 c) 400 - 162 d) 2.3.45.7.9.11.13 + 2018 e) 13 + 23
4. m) 1262 + 1 n) 100!+ 8 p) 1012 - 3 q) 1010 + 7 k) 11 + 112 + 113
Mọi người trình bày đầy đủ hộ mình ạ!
Nhanh giúp ạ
Đọc tiếp
Bài 2: Các số sau có phải là số chính phương không?
1. 13 + 23 ; 13 + 23 + 33 ; 13 + 23 + 33 + 43 ; 13 + 23 + 33 + 43 + 53
2. 1262 + 1 ; 100! + 8 ; 1012 - 3 ; 1010 + 7 ; 11 + 112 + 113
3. 32 + 22 b) 62 + 82 c) 400 - 162 d) 2.3.45.7.9.11.13 + 2018 e) 13 + 23
4. m) 1262 + 1 n) 100!+ 8 p) 1012 - 3 q) 1010 + 7 k) 11 + 112 + 113
Mọi người trình bày đầy đủ hộ mình ạ!
Nhanh giúp ạ
Bài 1:
13 + 23 = 1 + 8 = 9 = 32 (là một số chính phương)
13 + 23 + 33 = 1 + 8 + 27 = 36 = 62 (là một số chính phương)
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102 (là số cp)
13 + 23 + 33 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225 = (15)2 là số cp
Đúng 1
Bình luận (0)
Bài 2:
1262 + 1 = \(\overline{..6}\) + 1 = \(\overline{...7}\) (không phải số chính phương)
100! + 8 = \(\overline{...0}\) + 8 = \(\overline{...8}\) (không phải là số chính phương)
1012 - 3 \(\overline{..01}\) - 3 = \(\overline{...8}\) (không phải là số chính phương)
107 + 7 = \(\overline{..0}\) + 7 = \(\overline{..7}\) (không phải là số chính phương)
11 + 112 + 113 = \(\overline{..1}\)+ \(\overline{..1}\)+ \(\overline{..1}\) = \(\overline{...3}\) (không phải số chính phương)
Đúng 1
Bình luận (0)
Bài 3:
32 + 22 = 9 + 4 = 13 (không phải là số chính phương)
62 + 82 = 36 + 64 = 100 = 102 (là số chính phương)
2.3.45.7.9.11.13 + 2018 = \(\overline{...0}\) + 2018 = \(\overline{..8}\) (không phải là số cp)
Bài 4 giống bài 2
Đúng 0
Bình luận (0)
Số chính phương là số bằng bình phương của một số tự nhiên (ví dụ 0, 1, 4, 9, 16, ...). Mỗi tổng sau có là một số chính phương không?
13 + 23 + 33 + 43
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100.
Mà 100 = 102 là SCP (vì là bình phương của 10) nên 13 + 23 + 33 + 43 là SCP.
Vậy mỗi tổng đã cho đều là số chính phương.
Đúng 1
Bình luận (0)
Chứng minh:
1
3
+
2
3
1
+
2
Viết tiếp một số đẳng thức tương tự.
1
3
+
2
3...
Đọc tiếp
Chứng minh: 1 3 + 2 3 = 1 + 2
Viết tiếp một số đẳng thức tương tự.
1 3 + 2 3 + 3 3 = 1 + 2 + 3 1 3 + 2 3 + 3 3 + 4 3 = 1 + 2 + 3 + 4
Bài 1. Cho 𝐴 3 + 32 + 33 + ⋯ + 330.
- Chứng minh rằng: 𝐴 ⋮ 13 và 𝐴 ⋮ 52.
- Hỏi A có phải là số chính phương không? Tại sao?
Đọc tiếp
Bài 1. Cho 𝐴 = 3 + 32 + 33 + ⋯ + 330.
- Chứng minh rằng: 𝐴 ⋮ 13 và 𝐴 ⋮ 52.
- Hỏi A có phải là số chính phương không? Tại sao?
viết các tổng sau thành một bình phương a 13 23 33 43 53b 13 23 33 43 53 63
Xem chi tiết
Chứng minh rằng : 23^5 +23^12+23^2003 không phải là số chính phương
đầu tiên chứng minh là mày không bị thiểu năng bằng cách xóa câu hỏi này đi nhé
Viết các tổng sau thành một bình phương của một Số tự nhiên:a)
2
+
3
3
+
4
2
+
13
2
b)
1
3
+...
Đọc tiếp
Viết các tổng sau thành một bình phương của một Số tự nhiên:
a) 2 + 3 3 + 4 2 + 13 2
b) 1 3 + 2 3 + 3 3 + 4 3 + 5 3 + 6 3
a) 2 + 3 3 + 4 2 + 13 2 = 196 = 14 2
b, 1 3 + 2 3 + 3 3 + 4 3 + 5 3 + 6 3 = 441 = 21 2
Đúng 0
Bình luận (0)
Số chính phương là số bằng bình phương của một số tự nhiên (ví dụ 0, 1, 4, 9, 16, ...). Mỗi tổng sau có là một số chính phương không?
13 + 23 + 33
13 + 23 + 33 = 1 + 8 + 27 = 36.
Mà 36 = 62 là SCP (vì là bình phương của 6) nên 13 + 23 + 33 là SCP
Đúng 1
Bình luận (0)