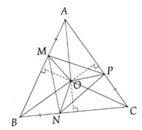
cho tam giác ABC cân tại A,lấy các điểm P,Q tương ứng trên các cạnh CA,CB sao cho PQ//AB.Gọi M là trung điểm BP,N là giao điểm các đường trung trực của tam giác CPQ. Chứng minh góc AMN=90 độ

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Lấy điểm P, Q tương ứng trên AC và BC sao cho PQ // AB. Gọi M là trung điểm của PB, N là giao điểm các đường trung trực của tam giác CPQ. Chứng minh: AMN = 90.
Gọi K là giao điểm của AM và PQ.
(Giờ ta chứng minh hai ý: Tứ giác APKB là hình bình hành và AN = NK).
Xét \(\Delta AMB\) và \(\Delta KMP\), ta có:
\(\widehat{AMB}=\widehat{KMP}\) (đối đỉnh).
BM = MP (M là trung điểm của PB).
\(\widehat{ABM}=\widehat{KPM}\) (Vì PQ // AB).
Do đó: \(\Delta AMB=\Delta KMP\left(g.c.g\right)\).
=> AM = MK.
Xét tứ giác APKB, ta có:
\(AM=MK=\dfrac{1}{2}AK\left(cmt\right)\)
\(BM=MP=\dfrac{1}{2}PB\left(gt\right)\)
Do đó: Tứ giác APKB là hình bình hành. (Xong 1 ý!!!).
Ta có:
\(\widehat{KBQ}=\widehat{ACB}\) ( Vì tứ giác APKB là hình bình hành).
\(\widehat{KQB}=\widehat{PQC}\) (đối đỉnh).
\(\widehat{ACB}=\widehat{ABC}\) (Tam giác ABC cân tại A).
\(\widehat{PQC}=\widehat{ABC}\) (PQ // AB).
Do đó: \(\widehat{KBQ}=\widehat{KQB}\)
=> \(\Delta BKQ\) cân tại K => KB = KQ.
Vì tứ giác APKB là hình bình hành (cmt) nên AP = KB.
Vậy KQ = AP.
Ta có: \(\widehat{APN}+\widehat{NPC}=180^o\left(1\right)\)
\(\widehat{NQK}+\widehat{NQP}=180^o\left(2\right)\)
Lại có: \(\widehat{PQC}=\widehat{PCQ}\left(=\widehat{ABC}\right)\)=> \(\Delta PQC\) cân tại P.
Do đó: PN là đường trung trực của \(\Delta PQC\).
Khi đó: PN là phân giác của \(\widehat{QPC}\) => \(\widehat{NPQ}=\widehat{NPC}\)
Lại có: \(\widehat{NPQ}=\widehat{NQP}\) (N là giao điểm các đường trung trực của \(\Delta CPQ\)).
Do đó: \(\widehat{NQP}=\widehat{NPC}\left(3\right)\)
Từ (1), (2) và (3) => \(\widehat{APN}=\widehat{NQK}\)
Xét \(\Delta APN\) và \(\Delta KQN\), ta có:
AP = KQ (cmt).
\(\widehat{APN}=\widehat{KQN}\left(cmt\right)\).
NP = NQ (N là giao điểm các đường trung trực của \(\Delta CPQ\)).
Do đó: \(\Delta APN=\Delta KQN\left(c.g.c\right)\)
=> AN = NK => \(\Delta ANK\) cân tại N.
Lại có: MN là trung tuyến của \(\Delta ANK\left(AM=MK\right)\)(cmt)
Vậy MN là đường cao của \(\Delta ANK\)
Do đó: \(\widehat{AMN}=90^o\left(đpcm\right).\)
Đúng 1
Bình luận (0)
Mn giúp mk bài này vs ạBài toán 1: Cho tam giác ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm 0 cách đều 3 đỉnh của tam giác ABC. Bài toán 2: Cho tam giác cân ABC (AB AC). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.Bài toán 3: Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM BN CP.a) Chứng minh tam giác MNP là tam giác đều b) Gọi O là giao điểm các đư...
Đọc tiếp
Mn giúp mk bài này vs ạ
Bài toán 1: Cho tam giác ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm 0 cách đều 3 đỉnh của tam giác ABC.
Bài toán 2: Cho tam giác cân ABC (AB = AC). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.
Bài toán 3: Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM = BN = CP.
a) Chứng minh tam giác MNP là tam giác đều b) Gọi O là giao điểm các đường trung trực của tam giác ABC. Chứng minh rằng 0 cũng là
giao điểm của các đường trung trực của tam giác MNP.
im đi Lê Minh Phương
kệ mẹ tao, thằng điên
Xem thêm câu trả lời
Cho tam giác ABC cân tại A, O là giao điểm các đường trung trực. Trên tia đối của tia AB và CA lấy điểm M và N sao cho AM = CN
a) Chứng minh góc OAB = góc OCA
b) Chứng minh tam giác AOM = tam giác CON
c) Gọi I là giao điểm hai đường trung trực của OM và ON. Chứng minh OI là phân giác của góc MON
1. Cho tam giác ABC cân tại đỉnh A trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC) trên tia đối tia AD lấy E sao cho AEBD chứng minh tam giác DCE cân gợi ý cần chứng minh CDCE2.cho tam giác ABC có AB AC lấy điểm E trên cạnh CA sao cho CEBA các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I a) chứng minh tam giác AIBtam giác CIEb) chứng minh tam giác AI là tia phân giác của góc BACGiups mk với !
Đọc tiếp
1. Cho tam giác ABC cân tại đỉnh A trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC) trên tia đối tia AD lấy E sao cho AE=BD chứng minh tam giác DCE cân gợi ý cần chứng minh CD=CE
2.cho tam giác ABC có AB < AC lấy điểm E trên cạnh CA sao cho CE=BA các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I a) chứng minh tam giác AIB=tam giác CIE
b) chứng minh tam giác AI là tia phân giác của góc BAC
Giups mk với !
1.Cho tam giác ABC vuông tại A. Các tia phân giác của góc B và góc C cắt nhau tại I. Gọi D, E, F là hình chiếu của I xuống AB, AC, BC.a) Chứng minh rằng ADAEb) Tính độ dài các đoạn thẳng AD, AE nếu biết AB 8cm, AC 15cmc) Trong trường hợp tam giác ABC cân tại A, hãy chứng minh rằng tam giác DEF là tam giác cân2.Cho tam giác ABC có ABAC. Trên tia đối của tia BC lấy điểm M sao cho BMBA, trên tia đối của tia CB lấy điểm N sao cho CNCAa) Hãy so sánh các góc AMB và ANCb) Hãy so sánh độ dài các đoạn...
Đọc tiếp
1.Cho tam giác ABC vuông tại A. Các tia phân giác của góc B và góc C cắt nhau tại I. Gọi D, E, F là hình chiếu của I xuống AB, AC, BC.
a) Chứng minh rằng AD=AE
b) Tính độ dài các đoạn thẳng AD, AE nếu biết AB = 8cm, AC = 15cm
c) Trong trường hợp tam giác ABC cân tại A, hãy chứng minh rằng tam giác DEF là tam giác cân
2.Cho tam giác ABC có AB<AC. Trên tia đối của tia BC lấy điểm M sao cho BM=BA, trên tia đối của tia CB lấy điểm N sao cho CN=CA
a) Hãy so sánh các góc AMB và ANC
b) Hãy so sánh độ dài các đoạn thẳng AM và AN
c) Gọi H là trung điểm của AM, K là trung điểm của AN. Hai đường thẳng BH và CK cắt nhau tại I. Chứng minh I là trực tâm của tam giác AMN
Cho tam giác ABC cân tại A. Gọi O là giao điểm các đường trung trực của tam giác. Trên tia đối của tia AB và CA lấy theo thứ tự hai điểm M và N sao cho AM=CN
a, Chứng minh góc OAB = góc OCA
b, Chứng minh tam giác AOM = tam giác CON
c, Gọi I là giao điểm hai đường trung trực của OM và ON. Chứng minh OI là tia phân giác của góc MON
Trên ba cạnh AB, BC và CA của tam giác đều ABC lấy các điểm theo thứ tự M, N, P sao cho AM BN CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC.a) Tính số đo góc
M
A
O
^
.b) Chứng minh
∆
M
A
O
∆
O
P
C
.
c) Chứng minh O là giao điểm ba đường trung trực của tam giác MNP.
Đọc tiếp
Trên ba cạnh AB, BC và CA của tam giác đều ABC lấy các điểm theo thứ tự M, N, P sao cho AM = BN = CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC.
a) Tính số đo góc M A O ^ .
b) Chứng minh ∆ M A O = ∆ O P C .
c) Chứng minh O là giao điểm ba đường trung trực của tam giác MNP.
Bài 1: Chứng minh định lí:a,Trong tam giác cân đường trung tuyến ứng với cạnh đáy cũng là đường phân giácb, Nếu một tam giác có đường trung tuyến ứng với một cạnh cũng là đường phân giác thì tam giác đó là tam giác cân.Bài 2; Cho tam giác ABC góc A90 độ. Trên cạnh AC lấy điểm D sao cho góc ABC 3 lần góc ABD . Trên cạnh AB lấy điểm E sao cho góc ACB 3 lần góc ACE .Gọi F là giao điểm BD và CE , I là giao điểm của các tia phân giác của tam giác BFCa,Tính BFCb,Chứng minh:Tam giác DEI là tam giác câ...
Đọc tiếp
Bài 1: Chứng minh định lí:
a,Trong tam giác cân đường trung tuyến ứng với cạnh đáy cũng là đường phân giác
b, Nếu một tam giác có đường trung tuyến ứng với một cạnh cũng là đường phân giác thì tam giác đó là tam giác cân.
Bài 2; Cho tam giác ABC góc A=90 độ. Trên cạnh AC lấy điểm D sao cho góc ABC =3 lần góc ABD . Trên cạnh AB lấy điểm E sao cho góc ACB = 3 lần góc ACE .Gọi F là giao điểm BD và CE , I là giao điểm của các tia phân giác của tam giác BFC
a,Tính BFC
b,Chứng minh:Tam giác DEI là tam giác cân
1. Cho tam giác ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC). Trên tia đối tia AD lấy E sao cho AEBD. Chứng minh tam giác DCE cân. (gợi ý: Cần chứng minh CDCE).2. Cho tam giác ABC có ABAC, lấy điểm E trên cạnh CA sao cho CEBA, Các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I.a, Chứng minh: tam giác AIB tam giác CIEb, Chứng minh: AI là tia phân giác của góc BAC.Các bạn ơi giúp mình với mình đang cần gấp lắm! pleas!!!
Đọc tiếp
1. Cho tam giác ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC). Trên tia đối tia AD lấy E sao cho AE=BD. Chứng minh tam giác DCE cân. (gợi ý: Cần chứng minh CD=CE).
2. Cho tam giác ABC có AB<AC, lấy điểm E trên cạnh CA sao cho CE=BA, Các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I.
a, Chứng minh: tam giác AIB= tam giác CIE
b, Chứng minh: AI là tia phân giác của góc BAC.
Các bạn ơi giúp mình với mình đang cần gấp lắm! pleas!!!