cho tam giác ABC vuông tại A đường cao AH,AB=9,BC=12.cho đường thẳng xy bất kì qua B .Từ C kẻ CN vuông với xy, từ A kẻ AM vuông với xy(N,M thuộc xy).Cm diện tích tam giác BNC16/9 diện tích AMB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại B , đường cao BH và AB=9 ; BC=12.
a) Tính AC ; BH
b) Chứng minh BC^2 = CH.AC
c) Vẽ đường thẳng xy bất kì qua B , từ C dựng CN và từ AC dựng AM cùng vuông góc với xy ( M và N thuộc xy). Chứng tỏ Stam giác AMB = 9/16 Stam giác BNC
Xét tam giác ABC vuông tại B có
AB^2 + BC^2 = AC^2
=> AC^2 = 9^2 + 12^2 =225
=> AC= 15
Xét tam giác AHB ~( đồng dạng) tam giác ABC (g.g)vì
AHB= ABC
chung A
=> BH/AB= BC/ AC
=>BH= 7,2
b,Xét tam giác CHB ~ tam giác CBA (g.g)
=> CH/ BC=BC/AC => BC^2= CH. AC(dpcm)
c,
Ta có B1 + ABC + B2= 180*
=> B1 + B2 = 90* (1)
Xét tam giác AMB vuông tại M
=> A1 +B1 = 90* (2)
Từ (1) và (2)=> B2= A1
Xét tam giác AMB ~ tam giác BNC (g.g)
=> S AMB / S BNC = AB^2 / BC^2 = 9^2 / 12 ^2 =9/16 (dpcm)
Đúng 1
Bình luận (0)
CHO TAM GIÁC ABC VUÔNG TẠI B, ĐƯỜNG CAO BH VÀ AB=9cm VÀ BC=12cm
a, CM: TAM GIÁC ABC ĐỒNG DẠNG VỚI TAM GIÁ AHB
b, CM: BC2 = CH.AC
c, qua B kẻ đường thẳng xy, từ C dựng CN và từ A dựng AM vuông góc với xy (N,M thuộc XY)
Cho tam giác ABC vuông tại B đường cao BH và AB = 9cm; BC = 12cm;
a,Tính AC và BH
b, Chứng minh BC2 = CH.AC
c, Vẽ đường thẳng xy bất kì qua B, từ C dựng CN và từ A dựng AM cùng vuông góc với xy(M và N thuộc xy). Chứng tỏ SAMB = \(\frac{9}{16}\) SBNC.
cho tam giác abc vuông tại a có ab=ac . qua a kẻ đường thẳng xy (b,c nằm cùng phía đối với xy) , kẻ bd và ce vuông góc vs xy. CMR :
b) de=bd+ce
c) lấy m thuộc bc sao cho am vuông góc với xy, biết góc bad = 60 độ và góc acb = 45 độ
Cho tam giác ABC vuông tại A, có ABAC, H là trung điểm của BC, M và N là hai điểm thuộc BC sao cho BMCN 1) CM:Delta ABHDelta ACHtừ đó tính các góc của tam giác ABC 2) CM: widehat{BAN}widehat{CAM} 3) Qua A kẻ đường thẳng xy bất kì sao cho B, C nằm cùng phía đối với xy. Kẻ BD và CE cùng vuông góc với xy (D,E thuộc xy). CM: DEBD+CE
Đọc tiếp
Cho tam giác ABC vuông tại A, có AB=AC, H là trung điểm của BC, M và N là hai điểm thuộc BC sao cho BM=CN
1) CM:\(\Delta ABH=\Delta ACH\)từ đó tính các góc của tam giác ABC
2) CM: \(\widehat{BAN}=\widehat{CAM}\)
3) Qua A kẻ đường thẳng xy bất kì sao cho B, C nằm cùng phía đối với xy. Kẻ BD và CE cùng vuông góc với xy (D,E thuộc xy).
CM: DE=BD+CE
cho tam giác ABC vuông cân tại đỉnh A. Qua A kẻ đường thẳng xy bất kỳ không cắt đoạn thẳng BC. kẻ BM và CN vuông góc với xy
a, CM tam giác ACN = tam giác BAN
b, CM CN + BM = MN
c, CM BM2 + CN2 không phụ thuộc vào vị trí của xy.
giúp mình giải bài này với!
a, ^NAC + ^BAC + ^MAB = 180 (kb)
^BAC = 90
=> ^NAC + ^MAB = 90
^NAC + ^NCA = 90
=> ^NCA = ^MAB
xét tam giác CNA và tam giác AMB có : AB = AC do tam giác ABC vc (gt)
^CNA = ^AMB = 90
=> tam giác CNA = tam giác AMB (ch-gn)
b, tam giác CNA = tam giác AMB (câu a)
=> NA = BM (đn) và CN = AM (đn)
có : NA + MA = MN
=> BM + CN = MN
c, NC = AM (câu b) => NC^2 = AM^2
xét tam giác MB vuông tại M => BM^2 + AM^2 = AB^2 (pytago)
=> BM^2 + NC^2 = AB^2
mà AB không phụ thuộc vào xy
=> BM^2 + CN^2 không phụ thuộc vào xy
b) de=bd+ce
Cho tam giác ABC đều. Qua B kẻ đường thẳng xy song song AC và hạ BM vuông góc với AC (M thuộc AC). Qua C kẻ đường thẳng xy song song AB và hạ CN vuông góc vói AB (N thuộc AB). Hai đường thẳng xy và xy cắt nhau tại P. Chứng minh:a) Đường phân giác của góc A và hai đường BM, CN đồng quy;b) Đường phân giác của góc A và hai đường thẳng xy và xy đồng quy.
Đọc tiếp
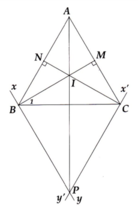
Cho tam giác ABC đều. Qua B kẻ đường thẳng xy song song AC và hạ BM vuông góc với AC (M thuộc AC). Qua C kẻ đường thẳng x'y' song song AB và hạ CN vuông góc vói AB (N thuộc AB). Hai đường thẳng xy và x'y' cắt nhau tại P. Chứng minh:
a) Đường phân giác của góc A và hai đường BM, CN đồng quy;
b) Đường phân giác của góc A và hai đường thẳng xy và x'y' đồng quy.
Cho tam giác ABC vuông tại A và AB=AC.Qua đỉnh A kẻ đường thẳng xy sao cho xy không cắt đoạn thẳng BC. Kẻ BD và CE vuông góc với xy(D thuộc xy,E thuộc xy)
a) CM. góc DAB= góc ACE
b)CM. tam giác ABD= tam giác CAE
c)CM. DE=BD+CE
a) Vì góc BAC = 90 độ(gt)
suy ra : Góc A1 + góc A2 = 90 độ (1)
Xét tam giác ACE , có :
góc A + góc C + góc E = 180 độ ( Áp dụng tổng 3 góc trong một tam giác )
hay góc A + góc C + 90 độ = 180 độ
suy ra : góc A + góc C =180 độ - 90 độ
suy ra : góc A + góc C = 90 độ (2)
Từ (1) và (2) , suy ra :
Góc A1 = góc C1 (ĐPCM)
b) Xét tam giác ABD và tam giác ACE . Có :
Góc A1 = Góc C1 (CMT)
AB = AC ( gt)
Góc ADB = Góc AEC ( vì cùng bằng 90 độ )
Suy ra : Tam giác ABD = Tam giác ACE ( cạnh huyền - góc nhọn ) (ĐPCM)
c) Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E . Có :
AB=AC(gt)
suy ra : BD = CE (1)
Mà : BD vuông góc với xy tại D (gt)(2)
CE vuông góc với xy tại E (gt)(3)
Từ (1), (2) và (3) . Suy ra :
DE = BD+CE ( ĐPCM)
Đúng 0
Bình luận (0)
hình thì các bạn bên dưới hoặc bên trên đã vẽ đúng hết rồi nha
Đúng 0
Bình luận (0)