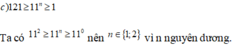Tìm số nguyên dương n biết 1/8.16^n

Những câu hỏi liên quan
Tìm giá trị n nguyên dương biết: 1/8.16^n=2^n
Bài 1: Tìm giá trị n nguyên dương biết:
a) 1/8.16^n=2^n
b) 27 < 3^n < 729
tìm giá trị n nguyên dương : a) 1/8.16n=2n
\(\frac{1}{8}.16^n=2^n\)
\(\frac{1}{2^3}.\left(2^4\right)^n=2^n\)
\(\frac{1}{2^3}.2^{4n}=2^n\)
\(\frac{1}{2^3}=2^n:2^{4n}\)
\(\frac{1}{2^3}=2^{n-4n}\)
\(\frac{1}{2^3}=2^{n\left(1-4\right)}\)
\(\frac{1}{2^3}=2^{\left(-3\right)n}\)
\(2^{\left(-3\right)n}.2^3=1\)
\(2^{\left(-3\right)n+3}=1\)
\(2^{3\left(-n+1\right)}=2^0\)
\(\Rightarrow3\left(-n+1\right)=0\)
\(\Rightarrow-n+1=0\)
\(-n=-1\)
\(n=1\)
Đúng 0
Bình luận (0)
tìm n để 1/8.16^n=2^n
Xem thêm câu trả lời
b, Tìm số nguyên dương n biết n-7:n+1 gấp nha!!!!
ta có:\(\frac{n-7}{n+1}=\frac{n+1-8}{n+1}=1-\frac{8}{n+1}\)
để \(n-7⋮n+1\Rightarrow\frac{n-7}{n+1}\in Z\)
\(\Rightarrow1-\frac{8}{n+1}\in Z\Leftrightarrow\frac{8}{n+1}\in Z\)
\(\Rightarrow n+1\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
do n nguyên dương nên \(\Rightarrow n+1\in\left\{1;2;4;8\right\}\)
bạn tính nốt n nhé
1)Tìm số nguyên dương n nhỏ nhất để \(3^n+3^{11}+3^{10}+3^8\) là 1 số chính phương
2)Tìm số nguyên dương n nhỏ nhất biết \(\sqrt{3^n+3^{11}+3^{10}+3^8}\) là số nguyên có 8 chữ số
Tìm n biết : 1!+ 2!+ 3!+ ....+ n! = 5913 với n là số nguyên dương
tìm số nguyên dương n biết 2.n+3 chia hết cho n-1
2.n+3 chia hết cho n-1
=>2n-3+6 chia hết cho n-1
=>2(n-1)chia hết cho n-1
=>6 chia hết cho n-1
=>n-1\(\inƯ\left(6\right)\)={1,-1,2,-2,3,-3,4,-4,6,-6}
=>\(n\in\left\{-5,-3,-2,-1,0,2,3,4,5,7,\right\}\)
@Thắng trước khi cậu làm cậu có nhìn đề bài cho điều kiện j ko vậy ? , chưa kể bài làm sai .
\(2n+3⋮n-1\)
\(2\left(n-1\right)+5⋮n-1\)
\(5⋮n-1\)
\(\Rightarrow n-1\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
| n - 1 | 1 | -1 | 5 | -5 |
| n | 2 | 0 | 6 | -4 |
Vì n là số nguyên dương
Nên n = 2;0;6
Brainchild làm đúng, nhưng Thắng thì làm sai
Tìm số nguyên dương n biết: 121 ≥ 11 n ≥ 1