Do phân giác trong của góc A và góc C cắt nhau tại I 

=> I là nội tiếp của tam giác ABC 

=> BI là phân giác góc B 

Do phân giác góc ngoài tại đỉnh A và C cắt nhau tại K 

Mà BI là phân giác góc B  ( tính chất phân giác góc trong và 2 phân giác ngoài trùng nhau ) 

=> B ; I ; K thẳng hàng 

Tham khảo nha !!! 

Cái này bạn đổi điểm K thành điểm M là xong nha

Kẻ IG,IK,IH lần lượt vuông góc với AB,BC,AC

Kẻ MO,MD,ME lần lượt vuông góc với AB,BC,AC

Xét ΔBKI vuông tại K và ΔBGI vuông tại G có

BI chung

góc KBI=góc GBI

Do đó: ΔBKI=ΔBGI

Suy ra: IK=IG(1)

Xét ΔCKI vuông tại K và ΔCHI vuông tại H có

CI chung

góc KCI=góc HCI

Do dó: ΔCKI=ΔCHI

Suy ra: IK=IH(2)

Từ (1) và (2) suy ra IG=IH

mà I nằm trong ΔABC và IG,IH là các đường cao ứng với các cạnh AB,AC

nên AI là phân giác của góc BAC(3)

Xét ΔBOM vuông tại O và ΔBDM vuông tại D có

BM chung

góc OBM=góc DBM

Do đó: ΔBOM=ΔBDM

Suy ra: MO=MD(4)

Xét ΔMDC vuông tại D và ΔMEC vuông tại E có

CM chung

góc DCM=góc ECM

Do đó: ΔMDC=ΔMEC

Suy ra: MD=ME(5)

Từ (4) và (5) suy ra MO=ME

mà M nằm ngoài ΔABC và MO,ME là các đường cao ứng với các cạnh AB,AC

nên AM là phân giác của góc BAC(6)

Từ (3) và (6) suy ra A,I,M thẳng hàng

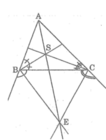
Ta có: BS ⊥ BE (tính chất đường phân giác của hai góc kề bù)

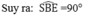
Và CS ⊥ CE (tính chất đường phân giác của hai góc kề bù)

Xét tứ giác BSCE ta có:

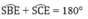
Vậy tứ giác BSCE nội tiếp đường tròn

+) Góc BDC là góc ngoài của tam giác ABD tại đỉnh D => góc BDC = góc A + góc ABD = góc A + góc \(\frac{B}{2}\)

+) Góc CEA là góc ngoài của tam giác BEC tại đỉnh E => góc CEA = góc B + góc BCE = góc B + góc \(\frac{C}{2}\)

Để góc BDC = góc CEA <=> góc A + góc \(\frac{B}{2}\) = góc B + góc \(\frac{C}{2}\) <=> góc A = góc \(\frac{B}{2}\) + góc \(\frac{C}{2}\) = \(\frac{B+C}{2}\)

=> B + C = 2.A 

Mà góc A + B + C = 180^o  nên góc A + 2.A = 180^o => 3.A = 180^o => góc A = 60^o

Vậy,.,,,,,