vẽ đồ thị hàm số y=-1/3x trên cùng một mặt phẳng tọa độ

Những câu hỏi liên quan
a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ y=3x và y= -\(\frac{1}{3}\)x
b) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ y=0,5x và y= -2x
a) vẽ đồ thị hàm số y=3x+3 và y=-1/2 x +1 trên cùng một mặt phẳng tọa độ . b) xác định cùng mặt phẳng tọa độ
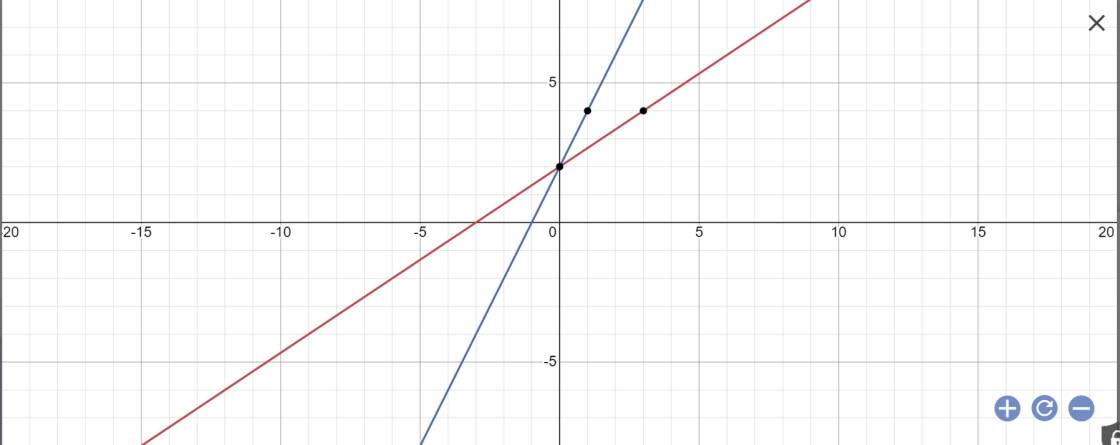
1) Trên cùng 1 mặt phẳng tọa độ hãy vẽ đồ thị các hàm số sau ; y=3x và y=x+2 2) tìm tọa độ giao điểm của đồ thị 3 hàm số vừa vẽ ở câu 1
2. PT hoành độ giao điểm: \(3x=x+2\Leftrightarrow2x=2\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow A\left(1;3\right)\)
Vậy \(A\left(1;3\right)\) là giao 2 đths
Đúng 0
Bình luận (0)
Vẽ đồ thị hàm số y=3x; y=1/2x; y=-x; y=-4/3x Trên cùng 1 mặt phẳng tọa độ
Xem chi tiết
Cho hai hàm số bậc nhất : y=2x+5 và y =x+3 A) vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ . b) tìm tọa độ giao điểm của đồ thị trên . c) tìm m để đường thẳng y=3x+m-3 đồng quy với đồ thị hai hàm số trên.
b: Tọa độ giao là:
2x+5=x+3 và y=x+3
=>x=-2 và y=1
c: Thay x=-2 và y=1 vào (d), ta được:
m-3-6=1
=>m=10
Đúng 0
Bình luận (0)
Cho hai hàm số y = x và y = 3x.
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm A, B của hai đồ thị trên lần lượt với đồ thị hàm số y = 3
c) Tính chu vi tam giác OBA
vẽ đồ thị hàm số d1:y=2/3x+2 và d2:y=2x+2 trên cùng 1 mặt phẳng tọa độ
Xem chi tiết
Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 3x + 6; (1) y = 2x + 4 (2)
y = x + 2; (3) y = 1/2x + 1. (4)
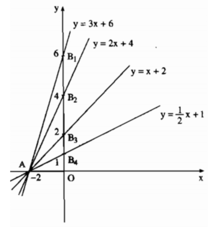
- Đồ thị của hàm số y = 3x + 6 là đường thẳng đi qua hai điểm A(-2;0) và B 1 (0;6).
- Đồ thị của hàm số y = 2x + 4 là đường thẳng đi qua hai điểm A(-2;0) và B 2 (0;4).
- Đồ thị của hàm số y = x + 2 là đường thẳng đi qua hai điểm A(-2;0) và B 3 (0;2).
- Đồ thị của hàm số y = 1/2x + 1 là đường thẳng đi qua hai điểm A(-2;0) và B 4 (0;1).
Đúng 0
Bình luận (0)
giải giúp mình bài này với
Cho hàm số y= -3x + 1 và y = -4/x
a. Vẽ đồ thị của 2 hàm số đó trên cùng 1 mặt phẳng tọa độ
b. Tìm tọa độ giao điểm của 2 đồ thị hàm số trên.
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{4}{x}=3x-1\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-x-4=0\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(3x-4\right)\left(x+1\right)=0\\y=3x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{\dfrac{4}{3};-1\right\}\\y\in\left\{3;-4\right\}\end{matrix}\right.\)
Đúng 0
Bình luận (0)