10² - 1 = 99 chia hết cho 99 rồi mà.

Mà n ở đâu vậy bạn?

nhầm nha CMR 10ⁿ - 1 chia hết cho 99 với n là số tự nhiên chẵn 

Ta có n là số tự nhiên nên n có 2 dạng : 2k hoặc 2k+1 (k\(\in\)N)

+Th1: n = 2k

\(\left(n+3\right)\left(n+6\right)=\left(2k+3\right)\left(2k+6\right)=2\left(2k+3\right)\left(k+3\right)⋮2\)

+Th2: n=2k+1

\(\left(n+3\right)\left(n+6\right)=\left(2k+4\right)\left(2k+7\right)=2\left(k+2\right)\left(2k+7\right)⋮2\)

Vậy với\(\forall n\in N\)thì tích (n+3)(n+6) chia hết cho 2

Ta có : 5 : 4 dư 1 suy ra 5 -1 chia hết cho 4

        5^2 :4 dư 1 suy ra 5^2 -1 chia hết cho 4

        5^3 :4 dư 1 suy ra 5^3 -1 chia hết cho 4

suy ra 5^n : 4 dư 1 suy ra 5^n - 1 chia hết cho 4

Vậy 5^n - 1 chia hết cho 4 với n thuộc N

tk mk nha

5 : 4 dư 1 thì 5ⁿ với n thuộc Z chia cho 4 cũng dư 1

=> Vậy nếu 5ⁿ - 1 thì tất nhiên Chia hết cho 4

mình nghĩ là nên dùng tình chất đồng dư

- Chắc là gọi thầy Nguyễn Việt Lâm thôi :)

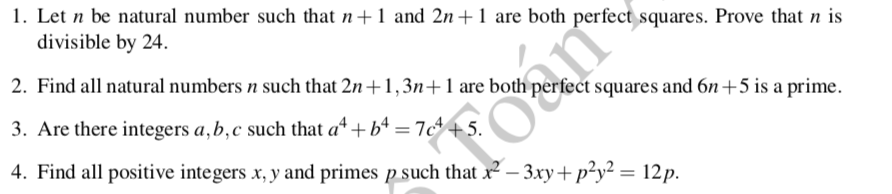
1.

\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)

\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ

\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)

\(\Rightarrow n=4b\left(b+1\right)\)

Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn

\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)

Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1

Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2

\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1

\(\Rightarrow n⋮3\)

\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau

2.

Lý luận tương tự bài 1, ta được n chẵn

Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4

Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2

\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1

\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)

\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)

- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)

- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)

Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu

2n+5chia hết cho 2n+1

=>4n+10chia hết cho 4n+2

=>2n+5chia hết cho 2n+1

Ta có: 2n + 5 = (2n - 1) + 6

Do 2n - 1 \(⋮\)2n - 1 => 6 \(⋮\)2n - 1

=> 2n - 1 \(\in\)Ư(6) = {1; 2; 3; 6}

=> 2n \(\in\){2; 3; 4; 7}

Do n \(\in\)N=> n \(\in\){1; 2}

Mình k cho bạn Edogawa Cona rùi nhé.Thanks

với dạng bài này ta phải tách số bị chia thành tổng hoặc hiệu 2 số trong đó có một số chia hết cho số chia

câu a)  2n +5 = 2n -1 +6

vì 2n -1 chia hết cho 2n -1  nên để 2n +5 chia hết cho 2n -1 khi 6 chia hết cho 2n -1

suy ra 2n -1 là ước của 6

vì 2n -1 là số lẻ nên 2n -1 \(\in\) {1;3}

n=1; 2