TOÁN 9:
cho tam giác ABC nội tiếp (o). Các đường phân giác trong của tam giác ABC cắt nhau tại I và cắt (o) theo thứ tự D,E,F.
a) Chứng minh tam giác DIC là tam giác cân
b) DE cắt AC tại K, DF cắt AB tại N. Chứng minh 3 điểm N,I,K thẳng hàng
Những câu hỏi liên quan
Cho tam giác ABC nội tiếp đường tròn tâm O . Các đường phân giác trong của góc A,B,C cắt nhau tại I và cắt đường tròn theo thứ tự D,E,F . DE cắt AC tại K . DF cắt AB tại N .
C/M: N,I,K thẳng hàng
Cho tam giác ABC nội tiếp đường tròn (O). Các tia phân giác góc B và C cắt nhau tại I và cắt (O) lần lượt tại D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minha) Các tam giác AMN, EAI và DAI là tam giác cânb) Tứ giác AMIN là hình thoi
Xem chi tiết
Cho tam giác ABC nội tiếp đường tròn (O). Các tia phân giác góc B và C cắt nhau tại I và cắt (O) lần lượt tại D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minha) Các tam giác AMN, EAI và DAI là tam giác cânb) Tứ giác AMIN là hình thoi
Xem chi tiết
cho tam giác ABC nhọn nội tiếp (O) kẻ phân giác trong của góc B và C cắt (O) tại thứ tự D,E và cắt nhau tại F .Gọi I, K theo thứ tự là giao điểm của DE với AB,AC
a) chứng minh tam giác EBF và DAF cân
b)DKFC nội tiếp và FK song song AB
c) AIFK là hình j vì sao
cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác góc A và B cắt hau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minha) tam BDI là tam giác cânb)DE là trung trực của ICc) IF và BC song song, trong đó F là giao điểm DE và AC
Xem chi tiết
cho tam giác ABC vuông tại A(AB<AC), tia phân giác góp ABC cắt AC tại D . vẽ DE vuông góc với BC tại E. Gọi F là giao điểm của đường thẳng AB và DE
a, Chứng minh tam giác ABD= tam giác EBD và tam giác CDF là tam giác cân
b, So sánh DE và DF
Mình cần câu b, thôi
a: XétΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D
b: Ta có: DE=DA
mà DA<DF
nên DE<DF
Đúng 1
Bình luận (0)
Bài 1: cho đường tròn (O;R) có dấy BC cố định. Một điểm A di động trên cung lớn BC. Gọi I là giao điểm 3 đường phân giác trong của tam giác ABC. Các tia AI,BI,CI cắt (O) lần lượt tại điểm thứ hai D,E,F. DE,DF cắt AB,AC theo thứ tự tại M,N. Chứng minh 3 điểm M,I,N thẳng hàngBài 2: Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại B và C với (O) cắt nhau tại M, đường thẳng AM cắt (O) tại N. Gọi P,Q lần lượt là giao điểm của đường thẳng vuông góc với NC tại C với (O) và BN. AP cắt BC tại E....
Đọc tiếp
Bài 1: cho đường tròn (O;R) có dấy BC cố định. Một điểm A di động trên cung lớn BC. Gọi I là giao điểm 3 đường phân giác trong của tam giác ABC. Các tia AI,BI,CI cắt (O) lần lượt tại điểm thứ hai D,E,F. DE,DF cắt AB,AC theo thứ tự tại M,N. Chứng minh 3 điểm M,I,N thẳng hàng
Bài 2: Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại B và C với (O) cắt nhau tại M, đường thẳng AM cắt (O) tại N. Gọi P,Q lần lượt là giao điểm của đường thẳng vuông góc với NC tại C với (O) và BN. AP cắt BC tại E. MO cắt PQ ở D. Chứng minh:
1) tứ giác AMBD nội tiếp
2) Ba điểm M,Q,E thẳng hàng
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:a, Tam giác BDI là tam giác cânb, DE là đường trung trực của ICc, IF và BC song song, trong đó F là giao điểm của DE và AC
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:
a, Tam giác BDI là tam giác cân
b, DE là đường trung trực của IC
c, IF và BC song song, trong đó F là giao điểm của DE và AC
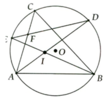
a, B I D ^ = 1 2 s đ D E ⏜ = D B E ^ => ∆BID cân ở D
b, Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D
=> EI = EC và DI = DC
=> DE là trung trực của CI
c, F Î DE nên FI = FC
=> F I C ^ = F C I ^ = I C B ^ => IF//BC
Đúng 1
Bình luận (0)
cho tam giác ABC nội tiếp đường tròn (o) phân giác góc A và B cắt nhau tại I và cắt (O) tại D và E, AC cắt DE tại F
a, chứng minh DE là trung trực của IC