cho tam giác abc có góc b tù trên cạnh bc lấy 2 điểm m và n sao cho bm=an CMR: ab+ac>am+an

Những câu hỏi liên quan
( Dùng trường hợp cạnh-góc-cạnh để chứng minh )
Cho tam giác ABC có : AB = AC, trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho : BM = CN
CMR: AM = AN
Trong \(\Delta ABC\)có: \(AB=AC\) (gt)
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(2 góc đáy)
Mà \(\widehat{ABC}+\widehat{ABM}=180^o\)
\(\widehat{ACB}+\widehat{ACN}=180^o\)
Nên \(\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\)và \(\Delta ACN\)có:
\(AB=AC\)(gt)
\(\widehat{ABM}=\widehat{ACN}\)(chứng minh trên)
\(MB=NC\)(gt)
Do đó \(\Delta ABM=\Delta ACN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A tù, AB AC. Trên cạnh BC lấy M và N sao cho BN BA, CM CA.a) So sánh
A
M
C
^
và
A
N
B
^
.b) So sánh AM và AN.c) Cho biết
A
B
C
^
40
°
,
A...
Đọc tiếp
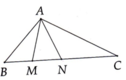
Cho tam giác ABC có góc A tù, AB < AC. Trên cạnh BC lấy M và N sao cho BN = BA, CM = CA.
a) So sánh A M C ^ và A N B ^ .
b) So sánh AM và AN.
c) Cho biết A B C ^ = 40 ° , A C B ^ = 30 ° .Tính ba góc tam giác AMN.
cho tam giác abc cân tại a ( góc a= 135 độ) trên cạnh bc lấy m,n sao cho am vuông góc với ac, an vuông góc với ab. cmr: bm^2=bc.mn
Số hs chiếm số phần trăm của cả khối 5 là: 100%-25%-5%=70%
Số học sinh giỏi cả khối 5 là: 126:70x25=45 (Hs)
Đáp số: 45 hs
Đúng 0
Bình luận (0)
Số hs chiếm số phần trăm của cả khối 5 là: 100%-25%-5%=70%
Số học sinh giỏi cả khối 5 là: 126:70x25=45 (Hs)
Đáp số: 45 hs
chúc bn hok tốt @_@
Đúng 0
Bình luận (0)
Cho tam giác ABC ; AB=AC; Trên tia đối BC lấy M sao cho: BM=BA ; Trên tia đối cb lấy N sao cho CN=CA
a/ CMR AM=AN
b/ Gọi I là trung điểm BC. CMR : BI là phân giác của góc MAN
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Trên cạnh BC lấy điểm M sao cho BM=BA. Trên cạnh AC lấy điểm N sao cho AN=AH. CMR:
a)MN vuông góc với AC
b)AN+BC>AB+AC
Help me!!!!!!!!!! ;-;
Ta có:
BM=BA
=> Tam giác ABM cân tại B
=> \(\widehat{BAM}=\widehat{BMA}\)
mà \(\widehat{BAM}+\widehat{MAC}=90^o\)
=> \(\widehat{BMA}+\widehat{MAC}=90^o\)
mặt khác \(\widehat{HMA}+\widehat{HAM}=90^o\)
=> \(\widehat{HAM}=\widehat{MAC}\)(1)
Ta có: AH=AN (2)
AM chung (3)
=>Tam giác AHM=ANM
=> \(\widehat{ANM}=\widehat{AHM}=90^o\)
=> AC vuông MN
b) => Tam giác MNC vuông tại N có cạnh huyền MC
=> MC>NC
=> AN+BC=BM+MC+AN=AB+MC+AN>AB+NC+AN=AB+BC
=> dpcm
Đúng 0
Bình luận (0)
Cho tam giác ABC có vuông tại A AH vuông góc BC cmr AH+BC>AB +AC
Cho tam giác ABC có góc A vuông với AB = 3cm; AC = 4cm; BC = 5 cm. Trên cạnh AB lấy điểm M sao cho AM = 2 cm, trên AC lấy điểm N sao AN = 1cm, trên cạnh BC lấy E sao cho BE = 2,5cm. Tìm S tam giác MNE
Tam giác ABC có AB = 6cm, AC = 8cm, BC = 11cm
a) Tính \(\overrightarrow{AB}.\overrightarrow{AC}\) và chứng tỏ rằng tam giác ABC có góc A tù
b) Trên cạnh AB lấy điểm M sao cho AM = 2cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow{AM}.\overrightarrow{AN}\) ?
a) Có \(\overrightarrow{BC}^2=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\overrightarrow{AC}.\overrightarrow{AB}\)
Suy ra: \(\overrightarrow{AC}.\overrightarrow{AB}=\dfrac{\overrightarrow{AC^2}+\overrightarrow{AB}^2-\overrightarrow{BC}^2}{2}=\dfrac{8^2+6^2-11^2}{2}=-\dfrac{21}{2}\).
Do \(\overrightarrow{AC}.\overrightarrow{AB}< 0\) nên \(cos\widehat{BAC}< 0\) suy ra góc A là góc tù.
b) Từ câu a suy ra: \(cos\widehat{BAC}=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=-\dfrac{21}{2.6.8}=-\dfrac{7}{32}\).
Do N là trung điểm của AC nên \(AN=AC:2=8:2=4cm\).
\(\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cos\left(\overrightarrow{AM},\overrightarrow{AN}\right)\)
\(=2.4.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=2.4.\dfrac{-7}{32}=-\dfrac{7}{4}\).
Đúng 0
Bình luận (0)
Trên 2 cạnh của tam giác ABC lấy M, N sao cho AN = BM = AB ( M thuộc AC; N thuộc BC ). Gọi P là giao điểm của AN và BM. Chứng minh: góc APM = 2 . góc ACB
Trên 2 cạnh của tam giác ABC lấy M, N sao cho AN = BM = AB ( M thuộc AC; N thuộc BC ). Gọi P là giao điểm của AN và BM. Chứng minh: góc APM = 2 . góc ACB