BÀI 3. Cho tam giác ABC. Trên tia đối của tia BC lấy M sao cho BM = BA. Trên tia đối tia CB lấy N sao cho CN = CA. Qua M kẻ đường thẳng song song với AB, qua N kẻ đường thẳng song song với AC, chúng cắt nhau tại P.
a) Chứng minh MA là tia phân giác của PMB , NA là tia phân giác của PNC . b) Chứng minh PA là tia phân giác của MNP .
c) Gọi D là trung điểm AM, E là trung điểm AN, các đường thẳng BD, CE cắt nhau tại Q. Chứng minh QM = QN.
d) Chứng minh ba điểm P, A, Q thẳng hàng.
\(\left(1-a+a^2\right)\left(1-b+b^2\right)=1-b+b^2-a+ab-ab^2+a^2-a^2b+a^2b^2.\)
\(=\frac{2-2a-2b+2b^2+2ab+2a^2-2ab\left(a+b\right)+2a^2b^2}{2}\)\(=\frac{\left(a-b\right)^2+1+a^2b^2+\left(1-a\right)^2\left(1-b\right)^2}{2}\ge\frac{1+a^2b^2}{2}\)
Tương Tự : \(\left(1-c+c^2\right)\left(1-d+d^2\right)\ge\frac{1+c^2d^2}{2}\)
(1-a+a2) (1-b+b2) = 1-b+b2-a+ab-ab2+a2-a2b+a2b2.
=2-2a-2b+2b2+2ab+2a2-2ab(a+b)+2a2b2 =(a-b)2+1+a2b2+(1-a)2(1-b)2> 1+a2b2 2 2 Tương Tự:(1-c+c2) (1-d+d2) > 1+c2d2 2
Cho tam giác ABC. Trên tia đối của tia BC lấy M sao cho BM = BA. Trên tia đối tia CB lấy N sao cho CN = CA. Qua M kẻ đường thẳng song song với AB, qua N kẻ đường thẳng song song với AC, chúng cắt nhau tại P.
a) Chứng minh MA là tia phân giác của P M B ^ , NA là tia phân giác của P N C ^ .
b) Chứng minh PA là tia phân giác của M N P ^ .
c) Gọi D là trung điểm AM, E là trung điểm AN, các đường thẳng BD, CE cắt nhau tại Q. Chứng minh QM = QN.
d) Chứng minh ba điểm P, A, Q thẳng hàng.
Cho tam giác ABC vuông tại A (AB<AC) trên tia đối của tia AB lấy điểm D sao cho AD =AB. chứng minh tam giác ABC = tam giác ADC. Gọi M là trung điểm BC đường thẳng qua B và song song với CD cắt DM tại K chứng minh BK = CD. Qua A kẻ đường thẳng song song với BC cắt CD tại M chứng minh tam giác AMC cân
Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
Hỏi lại cô cậu xem chứ mk tháy đè sai rồi đó
Cho tam giác ABC vuông tại A có AB < AC kẻ đường cao AH. Trên tia đối của tia AH lấy điểm D sao cho HD = HA a) Chứng minh tam giác ABH = tam giác DBH b) Chứng minh CB là tia phân giác góc ACD c) Qua A kẻ đường thẳng song song với BD, cắt cạnh BC tại E. Chứng minh DE // AB d) Đường thẳng AE cắt đường thẳng CD tại K. Chứng minh HK = 1/2AD
lam ho mk cau d
help me
Bài 1: Cho tam giác ABC có M là trung điểm cạnh BC. Trên tia đối của tia MA lấy D sao cho MA=MD. Tìm các tam giác bằng nhau có trên hình vẽ và chứng minh điều đó.
Bài 2: Cho hai điểm A và B nằm trên đường thẳng xy, trên cùng một nửa mặt phẳng bờ là đường thẳng xy ta kẻ hai đoạn AH và BK cùng vuông góc với xy sao cho AH=BK. a) Chỉ ra hai tam giác bằng nhau và chứng minh. b) Chỉ ra các cạnh các góc tương ứng. c) Gọi O là trung điểm HK. So sánh hai tam giác AOH và BOK.
Bài 3: Cho ABC, trên tia đối của tia AB, xác định điểm D sao cho AD = AB. Trên tia đối của tia AC xác định điểm E sao cho AE = AC. Chứng minh rằng: a) BC // ED b) DBC = BDE
Bài 4: Cho hai đoạn AB và CD cắt nhau tại trung điểm O của mỗi đường. Chứng minh BC // AD.
Bài 5: Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC ở D. Chứng minh: a) DB = DC b) AD BC
Bài 6: Cho tam giác ABC có AB = AC, M là trung điểm của BC, trên tia AM lấy D sao cho AM = MD. Chứng minh: a) ABM = DCM. b) AB // DC. c) AM BC
Bài 7: Qua trung điểm M của đoạn AB vẽ đường thẳng d vuông góc với AB. Trên đường thẳng d lấy điểm K. Chứng minh KM là tia phân giác của góc AKB.
Bài 8: Cho góc xOy có Ot là tia phân giác. Trên hai tia Ox, Oy lần lượt lấy các điểm M, N sao cho OM = ON. Trên tia Ot lấy P bất kì. Chứng minh a) PM = PN. b) Khoảng cách từ P đến hai cạnh của góc xOy bằng nhau.
Bài 9: Cho tam giác ABC có góc A bằng 90 0 . Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. a) Chứng minh: AB = DE b) Tính số đo góc EDC?
Bài 10: Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng bờ là đường thẳng BC không chứa điểm A vẽ tia Cx song song với AB. Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh: a) MA = MD b) BA điểm A, M, D thẳng hàng.
11: Cho tam giác ABC, M, N là trung điểm của AB và AC. Trên tia đối của tia NM xác định điểm P sao cho NP = MN. Chứng minh: a) CP//AB b) MB = CP c) BC = 2MN
Cho tam giác ABC, trên tia đối của tia BC lấy điểm M sao cho MB = AB, trên tia đối của tia CB lấy điểm N sao cho NC = AC. Qua M kẻ đường thẳng song song với AB. Qua N kẻ đường thẳng song song với AC. Hai đường thẳng đó cắt nhau tại P. Chứng minh:
a) MA, NA lần lượt là tia phân giác của P M B ^ , P N C ^
b) Tia PA cắt BC tại K. Chứng minh PA là tia phân giác của M P N ^ , từ đó suy ra AK là tia phân giác của B A C ^
Cho tám giác ABC có M là trung điểm của BC. Trên tia đối AM lấy điểm D sao cho M là trung điểm của AD: a) Chứng Minh tam giác ABM= tam giác DCM. b) Chứng minh AB song song CD. c) Qua C kẻ đường thẳng song song với AD cắt AB kéo dài tại E. Chứng minh A là trung điểm của BE
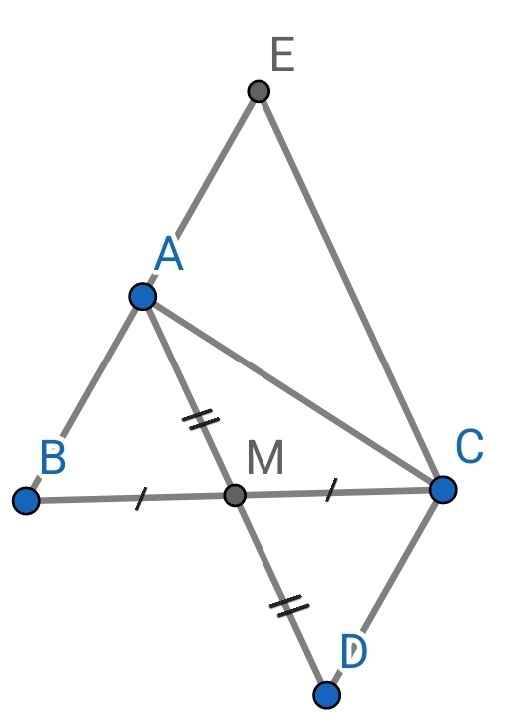a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a, chứng minh △AMB=△DMC
b, trên tia đối của tia CD, lấy điểm T sao cho CI=CA, qua điểm I vẽ đường thẳng song song AC cắt AB tại E. chứng minh △ACE là △ vuông cân
Giúp mình với ạaaa :3
Cho tam giác ABC vuông tại A có AB nhỏ hơn AC Gọi M là trung điểm của BC trên tia đối của tia MA lấy điểm D sao cho MA = MD
a) Chứng minh tam giác ABM bằng tam giác DCM. từ đó suy ra AB song song CD
b) Trên tia đối của tia CB lấy điểm E sao cho AD = AE Gọi I là trung điểm của AE chứng minh góc CAI bằng góc CEI và tính số đo của góc CAE
c) Kẻ AH vuông góc với BC sao cho H thuộc BC Qua E kẻ đường song song với AC đường thẳng này cắt đường thẳng tại F chứng minh AF = BC
Giúp minh nha
