Cho \(\Delta\)ABC nhọn có góc A = 30 độ, trên nửa mặt phẳng bờ BC không chứa điểm A vẽ \(\Delta\)đều BCD.Chứng minh :\(AD^2=AB^2+AC^2\)

Những câu hỏi liên quan
Cho tam giác ABC nhọn có góc A = 30 độ, trên nửa mặt phẳng bờ BC không chứa điểm A vẽ tam giác đều BCD.Chứng minh: AD2=AB2+AC2

Trên nửa mặt phẳng bờ AB không chứa C và D vẽ tam giác đều ABF
Xét \(\Delta ABD\)và \(\Delta FBC\)có:
AB = AF (tam giác ABF đều)
\(\widehat{ABD}=\widehat{FBC}\)(cùng bằng \(60^0+\widehat{ABC}\))
BD = BC ( tam giác BCD đều)
Suy ra \(\Delta ABD\)\(=\Delta FBC\left(c-g-c\right)\)
\(\Rightarrow AD=FC\)(hai cạnh tương ứng)
Ta có: \(\widehat{FAC}=\widehat{FAB}+\widehat{BAC}=60^0+30^0=90^0\)
Suy ra \(\Delta FAC\)vuông tại A\(\Rightarrow FC^2=FA^2+AC^2\)(Áp dụng định lý Py- ta -go)
\(\Rightarrow AD^2=FA^2+AC^2\)
\(\Rightarrow AD^2=AB^2+AC^2\)(AB = AF, hai cạnh của tam giác đều ABF)
Vậy \(\Rightarrow AD^2=AB^2+AC^2\)(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có góc A = 30 độ, trên nửa mặt phẳng bờ BC không chứa điểm A vẽ tam giác đều BCD.Chứng minh: AD2=AB2+AC2
cho tam giác ABC có góc A bằng 30 độ , trên nửa mặt phẳng bờ BC không chứa điểm A vẽ tam giác đều BCD . Chứng minh rằng : AD^2 = AB^2 + AC^2
Tam giác ABC có góc A= 30 độ. Trên nửa mặt phẳng bờ BC không chứa điểm A vẽ tam giác đều BCD.
Chứng minh: AD2= AB2+AC2
https://h.vn/hoi-dap/question/216941.html
Xem tại link này nhé(mình gửi cho)
Học tốt!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Ủa bài này bn làm rồi còn đăng làm gì v?
https://olm.vn/hoi-dap/detail/3752148442.html
Câu hỏi của Doraemon-Toán lớp 7
????????????>3,14
Đúng 0
Bình luận (0)
Tham khảo tại : Câu hỏi của Nguyễn Hương Giang - Toán lớp 7 | Học trực tuyến
< https://h.vn/hoi-dap/question/213906.html >
hay [Toán 7] Chứng minh tam giâc
< http://hoctap.info/threads/21640-Toan-7-Chung-minh-tam-giac.html >
-Chúc bạn học tốt-
_Minh ngụy_
Đúng 0
Bình luận (0)
Tam giác ABC có góc A= 30 độ. Trên nửa mặt phẳng bờ BC không chứa điểm A vẽ tam giác đều BCD.
Chứng minh: AD2= AB2+AC2
Cho Delta ABC nhọn (AB AC). Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia cX song song với AB. Trên tia Cx, lấy điểm D sao cho CD AB.a) Chứng minh Delta ABCDelta DCBb) Chứng minh AC // BDc) Kẻ AHperp BC tại H, DCperp BK tại K. Chứng minh AH DK.d) Gọi I là trung điểm của BC. Chứng minh I là trung điểm của AD.
Đọc tiếp
Cho \(\Delta ABC\) nhọn (AB < AC). Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia cX song song với AB. Trên tia Cx, lấy điểm D sao cho CD = AB.
a) Chứng minh \(\Delta ABC=\Delta DCB\)
b) Chứng minh AC // BD\
c) Kẻ \(AH\perp BC\) tại H, \(DC\perp BK\) tại K. Chứng minh AH = DK.
d) Gọi I là trung điểm của BC. Chứng minh I là trung điểm của AD.
Cho \(\Delta ABC\) nhọn . Trên nửa mặt phẳng bờ AB , không chưa điểm C , lấy điểm D sao cho AD vuông góc AB ; AD = AB . Trên nửa mặt phẳng bờ AC , không chứa điểm B , lấy E sao cho AE vuông góc AC . Kẻ AH vuông góc BC , tia HA cắt DE tại K . Chứng minh K là trung điểm DE
Câu hỏi của Nguyễn Đức Hiếu - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
Đúng 0
Bình luận (0)
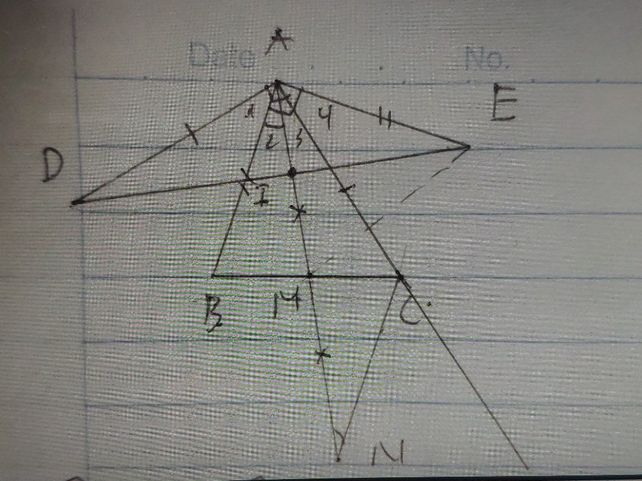
Cho tam giác ABC có ba góc nhọn, M là trung điểm của BC. Trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB vẽ đoạn thẳng AE vuông góc với AB và AE AB. Trên nửa mặt phẳng chứa điểm B bờ là đường thẳng AC vẽ đoạn thẳng AD vuông góc với AC và AD AC.1, Chứng minh rằng BD CE2, Trên tia đối của tia MA lấy điểm N sao cho MN MA. Chứng minh rằng : Delta ADEDelta CAN3, Gọi I là giao điểm của DE và AM. Chứng minh rằng frac{AD^2+IE^2}{DI^2+AE^2}1
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, M là trung điểm của BC. Trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB vẽ đoạn thẳng AE vuông góc với AB và AE = AB. Trên nửa mặt phẳng chứa điểm B bờ là đường thẳng AC vẽ đoạn thẳng AD vuông góc với AC và AD = AC.
1, Chứng minh rằng BD = CE
2, Trên tia đối của tia MA lấy điểm N sao cho MN = MA. Chứng minh rằng : \(\Delta ADE=\Delta CAN\)
3, Gọi I là giao điểm của DE và AM. Chứng minh rằng \(\frac{AD^2+IE^2}{DI^2+AE^2}=1\)
Bài làm nè bạn nhớ k mình nha

Cho \(\Delta ABC\)nhọn. Trên nửa mặt phẳng bờ AB không chứa C dựng đoạn thẳng AD vuông góc với AB và AD=AB. TRên nửa mặt phẳng bờ AC không chứa điểm B ta dựng đoạn thẳng AE vuông góc với AC và AE = AC. Vẽ AH vuông góc với BC. ĐƯờng thẳng HA cắt DE ở K. CMR: K là trung điểm của DE
Hình đẹp lắm lè
kẻ DO _|_ AH tại O
EI _|_ AH tại I
có góc OAD + góc BAD + góc BAH = 180
góc BAD = 90 do AD _|_ AB (gt)
=> góc OAD + góc BAH = 90 (1)
DO _|_ AH (Cách vẽ) => góc DOA = 90
=> góc ODA + góc DAO = 90 (2)
(1)(2) => góc ODA = góc BAH
xét tam giác ODA và tam giác HAB có : góc BHA = góc DOA = 90
AD = AB (gt)
=> tam giác ODA = tam giác HAB (ch - gn)
=> DO = AH (định nghĩa) (3)
làm tương tự với tam giác AHC và tam giác EIA
=> AH = EI (4)
(3)(4) => DO = EI
có EI; DO _|_ AH (cách vẽ)=> EI // DO => góc IEK = góc KDO (định lí)
xét tam giác ODK và tam giác IEK có : góc DOK = góc EIK = 90
=> tam giác ODK = tam giác IEK (cgv - gnk)
=> DK = KE mà K nằm giữa D và E
=> K là trung điểm của DE
Đúng 0
Bình luận (1)
trường hợp cgv-gnk là trường hợp cạnh góc vuông-góc nhọn kế với cạnh góc vuông đó.