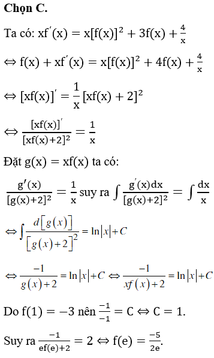cho f(x) thỏa mãn f(x)+xf(-x )=x+1 với mọi x. Tính f(1)

Những câu hỏi liên quan
a) Cho đa thức f(x)= 5.f(-2).x2 thỏa mãn với mọi x. Tính f(-3)
b) Cho f(x) thỏa mãn: f(x) + x.f(-x)=x+1 với mọi x. Tính f(-1)
c) Cho f(x)= ax2 + bx + c thỏa mãn f(1)=f(-1). Chứng minh rằng: f(x)=f(-x)
Giúp mình nha. Mình cảm ơn trước nhé :P
cho đa thức thỏa mãn: 2f(x)-xf(-x)=x+10 với mọi x thuộc R. tính f(2)
Với \(x=2\): \(2f\left(2\right)-2f\left(-2\right)=2+10=12\)
Với \(x=-2\): \(2f\left(-2\right)+2f\left(2\right)=-2+10=8\)
Cộng hai phương trình trên vế với vế ta được:
\(4f\left(2\right)=20\Leftrightarrow f\left(2\right)=5\)
Cho hàm số yf(x) có đạo hàm dương trên [1;2] thỏa mãn
f
(
1
)
1
e
và
x
f
(
x
)
+
(
x
+
1
)
f
(
x
)
3
x
2
e
-
x
. Tính f(2) A.
f
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm dương trên [1;2] thỏa mãn f ( 1 ) = 1 e và x f ' ( x ) + ( x + 1 ) f ( x ) = 3 x 2 e - x . Tính f(2)
A. f ( 2 ) = 1 e 2
B. f ( 2 ) = 2 e 2
C. f ( 2 ) = 4 e 2
D. f ( 2 ) = 8 e 2
cho đa thức f[x] thỏa mãn điều kiện : 3f[x] - xf[-x]= x+9 với mọi x thuộc R.Tính f[3]
cho đa thức thỏa mãn : 2f(x)-xf(-x)=x+10 với mọi x thuộc R. tính f(2)
Với x=10, ta có:
2. f(10)- 10. f(-10)=10+10
2f(10)-10f(-10)=20 (1)
Với x=-10. ta có:
2. f(-10)+10 f(10)=-10+10=0
=> 2 f (-10)=-10 f(10)
=> f(-10)=-5 f(10) (2)
Thay f(-10) từ PT (2) vào PT (1). ta có:
2f(10)-10f(-10)=20
<=> 2f(10) -10. (-5 f(10))=20
<=> 2 f(10)+50f(10)=20
<=> 52 f(10)=20
=> f(10)= 5/13
Cho hàm số yf(x) xác định và liên tục trên [1;e] thỏa mãn
xf
(
x
)
x
[
f
(
x
)
]
2
+
3
f
(
x
)
+
4
x
và f(1) -3. Tính f(e). A.
5
2
e
B. -...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Cho đa thức f(x) thỏa mãn: f(x)+x*f(-x)=x+1 với mọi x. Tính f(x)
Cho đa thức f(x) thỏa mãn: f(x) + x,f(-x) = x+1 với mọi x. Tính f(3)
Cho hàm số y=f(x) thoả mãn f(x)+xf(x/2x-1)=2 mọi x\{1;1/2}. Tính f(5)