Hãy khám phá “bí mật” của hình vuông rồi điền nốt bốn số tự nhiên còn thiếu vào ô trống.

Những câu hỏi liên quan
Hãy khám phá “bí mật” của hình vuông rồi điền nốt bốn số tự nhiên còn thiếu vào ô trống.
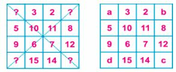
“Bí mật” của hình vuông là tổng các số hàng ngang, hàng dọc và đường chéo của hình vuông đều bằng 34 (các bạn tự kiểm tra lại).
Gọi các số cần tìm ở 4 góc của hình vuông là a, b, c, d. ở hàng ngang đầu tiên, ta có : a + 3 + 2 + b = 34, từ đó a + b = 34 - 5 = 29 (1).
Ở cột dọc đầu tiên ta có : a + 5 + 9 + d = 34, từ đó a + d = 34 - 14 = 20 (2).
Từ (1) và (2) ta có : a + b - (a + d) = 29 - 20 = 9 hay b - d = 9 (3).
Ở một đường chéo, ta lại có : b + 6 + 11 + d = 34, từ đó b + d = 34 - 17 = 17 (4).
Từ (3) và (4) ta có : (b - d) + (b + d) = 9 + 17 hay b + b = 26 ; b = 13.
Vì b + d = 17 nên d = 17 - 13 = 4.
Vì a + b = 29 nên a = 29 - 13 = 16.
Ở đường chéo thứ hai, ta có a + 10 + 7 + c = 34 hay a + c = 34 - 17 = 17.
Từ đó c = 17 - 16 = 1. Thay a, b, c, d bằng các số vừa tìm được ta có hình vuông sau :
Đúng 0
Bình luận (0)
Hãy khám phá "bí mật" của hình vuông rồi điền nốt 4 số tự nhiên còn thiếu vào ô trống?
| 3 | 2 | ||
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 15 | 14 |
hãy khám phá bí mật của hình vuông rồi điền nốt 4 số tự nhiên còn thiếu vào ô trống
| a | 3 | 2 | b |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| d | 15 | 14 | c |
a=16;b=13;c=1;d=4
(Quy tac:tong cac so trong moi cột doc va cột ngang bang 34)
Tick minh nha Bao!!!
Đúng 0
Bình luận (0)
Bí mật : tổng các hàng và các cột đều bằng 34
| a | 3 | 2 | b |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| d | 15 | 14 | c |
còn bảng thì tự điền
Đúng 0
Bình luận (0)
Bài 40: Hãy khám phá “bí mật” của hình vuông rồi điền nốt bốn số tự nhiên còn thiếu vào ô trống.
tong cua hai hang cheo la :31
a=7;b=7;c=7;d=7
Đúng 0
Bình luận (0)
Bài giải:
“Bí mật” của hình vuông là tổng các số hàng ngang, hàng dọc và đường chéo của hình vuông đều bằng 34 (các bạn tự kiểm tra lại).
Gọi các số cần tìm ở 4 góc của hình vuông là a, b, c, d. ở hàng ngang đầu tiên, ta có: a + 3 + 2 + b = 34, từ đó a + b = 34 - 5 = 29 (1).
ở cột dọc đầu tiên ta có : a + 5 + 9 + d = 34, từ đó a + d = 34 - 14 = 20 (2).
Từ (1) và (2) ta có : a + b - (a + d) = 29 - 20 = 9 hay b - d = 9 (3).
ở một đường chéo, ta lại có : b + 6 + 11 + d = 34, từ đó b + d = 34 - 17 = 17 (4).
Từ (3) và (4) ta có : (b - d) + (b + d) = 9 + 17 hay b + b = 26 ; b = 13.
Vì b + d = 17 nên d = 17 - 13 = 4.
Vì a + b = 29 nên a = 29 - 13 = 16.
ở đường chéo thứ hai, ta có a + 10 + 7 + c = 34 hay a + c = 34 - 17 = 17.
Từ đó c = 17 - 16 = 1. Thay a, b, c, d bằng các số vừa tìm được ta có hình vuông sau:
Đúng 0
Bình luận (0)
Hãy khám phá “bí mật” của hình vuông rồi điền nốt bốn số tự nhiên còn thiếu vào ô trống.
Bài giải:
“Bí mật” của hình vuông là tổng các số hàng ngang, hàng dọc và đường chéo của hình vuông đều bằng 34 (các bạn tự kiểm tra lại).
Gọi các số cần tìm ở 4 góc của hình vuông là a, b, c, d. ở hàng ngang đầu tiên, ta có: a + 3 + 2 + b = 34, từ đó a + b = 34 - 5 = 29 (1).
ở cột dọc đầu tiên ta có : a + 5 + 9 + d = 34, từ đó a + d = 34 - 14 = 20 (2).
Từ (1) và (2) ta có : a + b - (a + d) = 29 - 20 = 9 hay b - d = 9 (3).
ở một đường chéo, ta lại có : b + 6 + 11 + d = 34, từ đó b + d = 34 - 17 = 17 (4).
Từ (3) và (4) ta có : (b - d) + (b + d) = 9 + 17 hay b + b = 26 ; b = 13.
Vì b + d = 17 nên d = 17 - 13 = 4.
Vì a + b = 29 nên a = 29 - 13 = 16.
ở đường chéo thứ hai, ta có a + 10 + 7 + c = 34 hay a + c = 34 - 17 = 17.
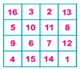
Từ đó c = 17 - 16 = 1. Thay a, b, c, d bằng các số vừa tìm được ta có hình vuông sau:
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Đúng 0
Bình luận (0)
Bài giải:
“Bí mật” của hình vuông là tổng các số hàng ngang, hàng dọc và đường chéo của hình vuông đều bằng 34 (các bạn tự kiểm tra lại).
Gọi các số cần tìm ở 4 góc của hình vuông là a, b, c, d. ở hàng ngang đầu tiên, ta có: a + 3 + 2 + b = 34, từ đó a + b = 34 - 5 = 29 (1).
ở cột dọc đầu tiên ta có : a + 5 + 9 + d = 34, từ đó a + d = 34 - 14 = 20 (2).
Từ (1) và (2) ta có : a + b - (a + d) = 29 - 20 = 9 hay b - d = 9 (3).
ở một đường chéo, ta lại có : b + 6 + 11 + d = 34, từ đó b + d = 34 - 17 = 17 (4).
Từ (3) và (4) ta có : (b - d) + (b + d) = 9 + 17 hay b + b = 26 ; b = 13.
Vì b + d = 17 nên d = 17 - 13 = 4.
Vì a + b = 29 nên a = 29 - 13 = 16.
ở đường chéo thứ hai, ta có a + 10 + 7 + c = 34 hay a + c = 34 - 17 = 17.
Từ đó c = 17 - 16 = 1. Thay a, b, c, d bằng các số vừa tìm được ta có hình vuông sau:
Nhận xét: Hình vuông trên gọi là hình vuông kì ảo (hoặc ma phương) cấp 4. Người ta đã nhìn thấy nó lần đầu tiên trong bản khắc của họa sĩ Đuy-rơ năm 1514. Các bạn có thể thấy : Tổng bốn số trong bốn ô ở bốn góc cũng bằng 34.
Ủng hộ nhé! >_<
Đúng 0
Bình luận (0)
“Bí mật” của hình vuông là tổng các số hàng ngang, hàng dọc và đường chéo của hình vuông đều bằng 34 (các bạn tự kiểm tra lại).
Gọi các số cần tìm ở 4 góc của hình vuông là a, b, c, d. ở hàng ngang đầu tiên, ta có: a + 3 + 2 + b = 34, từ đó a + b = 34 - 5 = 29 (1).
ở cột dọc đầu tiên ta có : a + 5 + 9 + d = 34, từ đó a + d = 34 - 14 = 20 (2).
Từ (1) và (2) ta có : a + b - (a + d) = 29 - 20 = 9 hay b - d = 9 (3).
ở một đường chéo, ta lại có : b + 6 + 11 + d = 34, từ đó b + d = 34 - 17 = 17 (4).
Từ (3) và (4) ta có : (b - d) + (b + d) = 9 + 17 hay b + b = 26 ; b = 13.
Vì b + d = 17 nên d = 17 - 13 = 4.
Vì a + b = 29 nên a = 29 - 13 = 16.
ở đường chéo thứ hai, ta có a + 10 + 7 + c = 34 hay a + c = 34 - 17 = 17.
Từ đó c = 17 - 16 = 1. Thay a, b, c, d bằng các số vừa tìm được ta có hình vuông sau:
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hãy khám phá “bí mật” của hình vuông rồi điền nốt bốn số tự nhiên còn thiếu vào ô trống.
hãy điền các số còn thiếu vào ô vuông trống sao cho hình vuông dưới là một hình vuông kì diệu ( cứu mik vs mn :< )
/.../21/26/
/23/.../27/
/24/.../22/
Hình vuông dưới đây có tính chất: mỗi ô ghi một luỹ thừa của 10; tích các ô trong mỗi hàng; cột; mỗi đường chéo đều bằng nhau. Hãy điền các số còn thiếu vào các ô trống:
100
10-5
102
103
Đọc tiếp
Hình vuông dưới đây có tính chất: mỗi ô ghi một luỹ thừa của 10; tích các ô trong mỗi hàng; cột; mỗi đường chéo đều bằng nhau. Hãy điền các số còn thiếu vào các ô trống:
| 100 | 10-5 | 102 |
| 103 |
Tích của mỗi hàng, cột, đường chéo là:
100.10-5.102 = 10–3
Từ đó ta điền được vào các ô trống còn lại như sau:
| 100 | 10-5 | 102 |
| 101 | 10-1 | 10-3 |
| 10-4 | 103 | 10-2 |
Đúng 0
Bình luận (0)
Điền số còn thiếu vào ô trống:
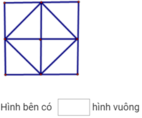
Trong hình đã cho có 4 vuông được ghép từ hai hình tam giác; 1 hình vuông được ghép từ 4 hình tam giác và 1 hình vuông to bên ngoài.
Vậy hình đã cho có tất cả 6 hình vuông.
Số cần điền vào chỗ trống là 6.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
















