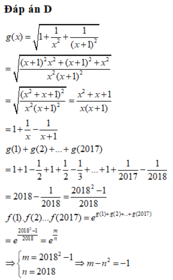cho hàm số f x xác định như sau Ứng với mỗi số tự nhiên có 3 chữ số là tổng các chữ số của số đóa,tính f 135 ,f 141 ,f 2017 b, tìm x biết f x 3

Những câu hỏi liên quan
Hàm số y = f (x) được xác định như sau: Ứng với mỗi số tự nhiên có ba chữ số là tổng các chữ số của số đã cho.
a) Tính f (124); f (212); f (999).
b) Tìm x, biết f (x) = 3.
Hàm số f được xác định như sau: cho ứng mỗi số ( tự nhiên) có 2 chữ số ta được hàm số f là tổng các chữ số của nó:
Tính f(12),f(29),f(73). tìm x biết f(x)=5.
Chỉ ra tập hợp các số x và tập hợp các số y của hàm số trên.
f(12)=3,f(29)=11,f(73)=10
x=14,23,32,41,-83,-38,-16,-27,-38,-49,-94.-83.-61
Đúng 0
Bình luận (0)
1) Cho hai hàm số y = f (x) và y = h (x) được xác định bởi công thức f (x) = [x] và h (x) = {x}.
Tính h(x) biết x∈{−4,2;−3,24;−1,15;−0,2;0,2;1,15;3,24;4,2}.
2) Hàm số y = f (x) được xác định như sau: Ứng với mỗi số tự nhiên có ba chữ số f(x) bằng tổng các chữ số của số đã cho.
Tính f (212).
f (x) = [x] = phần nguyên của x : là số nguyên lớn nhất nhỏ hơn x
h(x) = {x} = x - [x] = phần lẻ của x
1) x = -4,2 => [x] = -5 => h(-4,2) = {-4,2} = -4,2 - (-5) = 0,8
các số còn lại tương tự
Đúng 0
Bình luận (0)
Hàm số y= f(x) đợ xác định như sau: Ứng với mỗi số tự nhiên n là số dư của n khi chia cho 3
a)Tính f(124), f(2012), f(999)
b)Tìm x nếu f(x)= 3
cho hàm số f(x) được xác định như sau
Ứng với mỗi số tự nhiên n là số dư r khi n chia cho 3
a,tính f(124),f(2016),f(2016)
b,tìm x biết f(0)=0
hury up
toi chua ghet ban
hàm số f(x) được xác định như sau : cho tương ứng mỗi số tự nhiên có 2 cs với gttđ của hiệu hai cs của nó
a. tìm công thức xác định f(x)
b. tính f(72) , f(59) , f(66)
c. tìm x,y biết f(x)-f(y)=9
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị của hàm số
f
(
x
)
,
biết
f
(
3
)
+
f
(
2
)
f...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
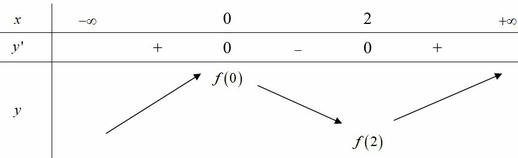
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
e
1
+
1
x
2
+
1
(
x
+...
Đọc tiếp
Cho hàm số f ( x ) = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f ( 1 ) . f ( 2 ) . f ( 3 ) . . . f ( 2017 ) = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m - n 2
A. m - n 2 = 2018
B. m - n 2 = 1
C. m - n 2 = -2018
D. m - n 2 = -1
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f(x), biết f(3)+f(20f(0)+f(1) và các khẳng định sau:1) Hàm số yf(x) có 2 điểm cực trị2) Hàm số yf(x) đồng biến trên khoảng
-
∞
;
0
3)
M
a
x
0
;
3
f...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5