Cho \(\Delta\)ABC có BC = 60 cm, chiều cao tương ứng = 40 cm. Gọi D,E là trung điểm AB, AC. Tính diện tích BDEC

Những câu hỏi liên quan
Cho tam giác ABC có đáy BC = 60 cm, chiều cao tương ứng 40 cm. Gọi D, E theo thứ tự là trung điểm của AB, AC. Tính diện tích tứ giác BDEC
Cho tam giác ABC ( vuông ở A ) . Có AB = 30 cm, AC = 40 cm ,BC = 50 cm . D và E trên AB và AC . Cho biết diện tích hình thang BDEC có chiều cao là 6 cm
a, Hãy tính 3 đường cao tam giác ABC
b,Tính diện tích tam giác ADE
Bài 2. 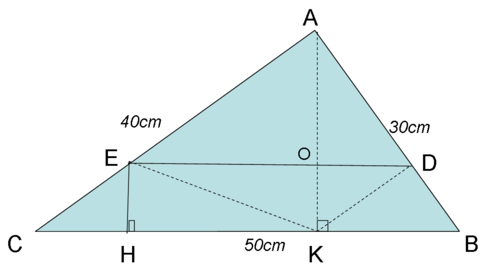
a) Trong tam giác vuông thì 2 cạnh góc vuông cũng chính là 2 đường cao của tam giác đó.
Vậy đường cao AB = 30 cm ; đường cao AC = 40 cm
Đường cao tam giác ABC còn lại đỉnh A là : 30 x 40 : 50 = 24 (cm)
b) S_ECK + S_DKB = CK x 6 : 2 + KB x 6 : 2 = (CK+KB) x 6 : 2 = 50 x 3 = 150 (cm2)
S_AEKD = 30 x 40 : 2 - 150 = 450 (cm2)
Xét tam giác AED và EDK chung đáy ED chiều cao AO = 24 - 6 = 18 (cm)
Tỉ lệ AO/OK = 18/6 = 3. Vậy S_AED = 3 x S_EDK
Diện tích tam giác AED là : 450 : (1+3) x 3 = 337,5 (cm2)
Đúng 0
Bình luận (0)
WTF!!!!!!!!!! Khó Zậy!!!
Cho tam giác ABC là tam giác vuông tại A, cạnh AB =30cm, cạnh AC =40 cm, cạnh BC =50cm. Trên AB lấy điểm D , trên AC lấy điểm E sao cho BDEC là hình thang vuông có chiều cao bằng 6 cm.
a)Tính độ dài 3 đường cao của tam giác ABC
b)Tính diện tích tam giác ADE
a, Chiều cao thứ nhất của tam giác ABC là AC= 40 cm
Chiều cao thứ hai của tam giác ABC là AB= 30 cm
Gọi chiều cao thứ ba của tam giác ABC là AI
Diện tích tam giác ABC là:
(40x30):2=600 ( cm 2)
Chiều cao AI là:
600x2:50=24 ( cm)
b,Nối B Với E
Diện tích tam giác BEC là
50 x 6 : 2=150 ( cm 2)
Diện tích tam giác BEA là
600-150=450 ( cm 2)
Độ dài đoạn thẳng DE là
450x2:30=30 ( cm)
Gọi AK là chiều cao của tam giác ADE
=>Độ dài chiều cao AK là:
24-4=20 ( cm)
Diện tích tam giác ADE là:
(20x30):2=300 ( cm 2)
Cho tam giác ABC vuông ở A, biết: AB = 30 cm, AC = 40 cm và BC =-x AC. Điểm D trên cạnh AB, điểm E trên cạnh AC sao cho hình thang BDEC có độ dài đường cao băng 9,6 cm và có hai đáy là DE và BC. a) Tính diện tích của hình tam giác ABC b) Tính diện tích của hình tam giác ADE
câu a mình chịu nhé
câu b: DIện tích tam giác ADE= 337,5 cm2
cho tam giác ABC có góc A vuông,cạnh AB bằng 40 cm, cạnh AC bằng 60 cm, EDAC là hình thang có chiều cao 10 cm. ( E ở trên cạnh BC, D ở trên cạnh AB ). Em hãy tính diện tích hình tam giác BED
cho tam giác ABc vuông ở A có cạnh AB bằng 60 cm , Ac bằng 80 cm,BC bằng 100 cm . trên cạnh AB lấy điểm D,trên cạnh AC lấy điểm E sao cho tứ giác BCED là hình thang có chiều cao là 30 cm. Tính diện tích hình thang BCED
ai giải nhanh có thưởng
Xem thêm câu trả lời
Cho hình vẽ bên trong đó ABCD là hình tam giác vuông ở a cạnh AB bằng 30 cm cạnh AC bằng 40 cm cạnh BC bằng 50 cm biết BDEC là hình thang có chiều cao bằng 6 cm :
a) tính độ dài 3 đường cao của tam giác ABC
b) tính diện tích ADE
a, Chiều cao thứ nhất của tam giác ABC là AC= 40 cm
Chiều cao thứ hai của tam giác ABC là AB= 30 cm
Gọi chiều cao thứ ba của tam giác ABC là AI
Diện tích tam giác ABC là:
(40x30):2=600 ( cm 2)
Chiều cao AI là:
600x2:50=24 ( cm)
b,Nối B Với E
Diện tích tam giác BEC là
50 x 6 : 2=150 ( cm 2)
Diện tích tam giác BEA là
600-150=450 ( cm 2)
Độ dài đoạn thẳng DE là
450x2:30=30 ( cm)
Gọi AK là chiều cao của tam giác ADE
=>Độ dài chiều cao AK là:
24-4=20 ( cm)
Diện tích tam giác ADE là:
(20x30):2=300 ( cm 2)
Cho \(\Delta ABC\) vuông tại A , đường cao AH . Biết BC = 5 cm , BH = 1,8 cm . Gọi M là trung điểm của BC , đường trung trực của BC cắt AC tại D .
a) Tính AB , AH
b) Tính tỉ số diện tích của \(\Delta DMC\) và \(\Delta ABC\)
c) Chứng minh : AC . DC = \(\frac{1}{2}BC^2\)
d) Tính diện tích tứ giác ADMB
\(\text{Hình bạn tự vẽ ^_^}\)
\(\text{a)Ta có: }AB^2=HB.BC=1,8.5=9\)
\(\Rightarrow AB=\sqrt{9}=3\left(\text{cm}\right)\)
\(\text{Lại có: }HC=BC-BH=5-1,8=3,2\left(\text{cm}\right)\)
\(\text{và: }AH^2=BH.CH=1,8.3,2=5,76\)
\(\Rightarrow AH=\sqrt{5,76}=2,4\left(\text{cm}\right)\)
\(\text{b) vì M là trung điểm BC nên }BM=CM=\frac{BC}{2}=\frac{5}{2}=2,5\left(\text{cm}\right)\)
\(\text{Ta lại có: }AC^2=CH.BC=3,2.5=16\)
\(\Rightarrow AC=\sqrt{16}=4\left(\text{cm}\right)\)
\(\text{Xét }\Delta DMC\text{ và }\Delta BAC\text{ có:}\)
\(\widehat{DMC}=\widehat{BAC}=90^o\)
\(\widehat{C}\text{ là góc chung}\)
\(\text{ }\Rightarrow\Delta DMC\text{ đồng dạng với }\Delta BAC\)
\(\Rightarrow\frac{DM}{AB}=\frac{DC}{BC}=\frac{CM}{AC}=\frac{2,5}{4}=0,625\left(\text{Tỉ số đồng dạng}\right)\)
\(\text{Vậy }\frac{S_{DMC}}{S_{BAC}}=\left(0,625\right)^2=\frac{25}{64}\)
Đúng 0
Bình luận (0)
a, \(AB=\sqrt{BH\cdot BC}=\sqrt{1,8\cdot5}=3\)
\(AH=\sqrt{AB^2-BH^2}=\sqrt{3^2-1,8^2}=2,4\)
b, \(\frac{S_{ABC}}{S_{DMC}}=\frac{MC^2}{BC^2}=\frac{1}{4}\)
c,\(\Delta ABC~\Delta MDC\Rightarrow\frac{BC}{DC}=\frac{AC}{MC}\Rightarrow AC\cdot CD=\frac{1}{2}BC^2\)
d,Cái này bạn tự tính nhá
Mk hơi lười nên làm hơi tắt có j thông cảm mk nha
Đúng 0
Bình luận (0)
Cho hình tam giác ABC có góc vuông A , cạnh AC = 12 cm , diện tích ABC = 54 cm vuông . E là trung điểm của BC , M là trung điểm của AB . AE cắt CM tại i . a) tính AB - b) So sánh diện tích AMi và diện tích eic - c) vẽ đường cao ik của aic tính ik
Từ đề bài, ta suy ra tỉ lệ các diện tích là:
SBAE = SACE = SMAC = SMBC
Độ dài AB là: 54 : (12 : 2) = 9 (cm)
Xét 2 tam giác MAC và ACE: Do đều có diện tích như nhau (cả 2 đều chiếm \(\dfrac{1}{2}\) diện tích ABC), chung tam giác AIC.
⇒ SAMI = SEIC
Nối B tới I, ta có được tam giác MBC được chia thành 3 phần bằng nhau ⇒ Mỗi phần sẽ có diện tích là: 27 : 3 = 9 (cm2)
Diện tích tam giác AIC là: 54 - 27 - 9 = 18 (cm2)
Độ đường cao IK là: 18 : (12 : 2) = 3 (cm)
Đáp số: a) 9cm
b) SAMI = SEIC
c) 3cm
Đúng 1
Bình luận (0)