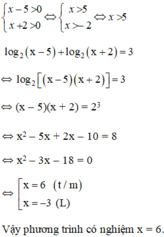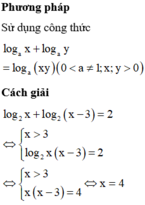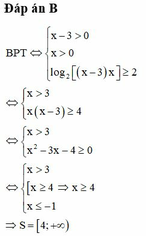2/(log2x -3)

Những câu hỏi liên quan
Giải các phương rình lôgarit: log 2 x - 5 + log 2 x + 2 = 3
Phương trình
log
2
x
+
log
2
x
-
3
2
có bao nhiêu nghiệm? A. 2 B. 0 C. 3 D. 1
Đọc tiếp
Phương trình log 2 x + log 2 x - 3 = 2 có bao nhiêu nghiệm?
A. 2
B. 0
C. 3
D. 1
Phương trình log 2 x + log 2 x − 3 = 2 có bao nhiêu nghiệm?
A. 2
B. 0
C. 3
D. 1
Phương trình
log
2
x
+
log
2
x
-
3
2
có bao nhiêu nghiệm? A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Phương trình log 2 x + log 2 x - 3 = 2 có bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 0
Phương trình log 2 x + log 2 x − 3 = 2 có bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 0
Tập nghiệm của bất phương trình
log
2
x
-
3
+
log
2
x
≥
2
là A.
3
;
+
∞
B.
4
;
+
∞
C.
-...
Đọc tiếp
Tập nghiệm của bất phương trình log 2 x - 3 + log 2 x ≥ 2 là
A. 3 ; + ∞
B. 4 ; + ∞
C. - ∞ ; - 1 ∪ 4 ; + ∞
D. 3 ; 4
Tập nghiệm S của phương trình
log
2
x
+
log
2
x
−
2
log
2
2
x
−
3
là A.
S
3
B.
S
1
;...
Đọc tiếp
Tập nghiệm S của phương trình log 2 x + log 2 x − 2 = log 2 2 x − 3 là
A. S = 3
B. S = 1 ; 3
C. S = ∅
D. S = 1
Đáp án A
PT ⇔ x > 0 x − 2 > 0 2 x − 3 > 0 log 2 x x − 2 = log 2 2 x − 3 ⇔ x > 2 x x − 2 = 2 x − 3 ⇔ x > 2 x 2 − 4 x + 3 = 0
⇔ x > 2 x = 1 x = 3 ⇒ x = 3 ⇒ S = 3
Đúng 0
Bình luận (0)
Cho hàm số
y
log
2
x
.
Xét các phát biểu(1) Hàm số
y
log
2
x
đồng biến trên khoảng (0;+∞) .(2) Hàm số
y
log
2
x
có một điểm cực tiểu.(3) Đồ thị hàm số
y
log
2
x
có tiệm cận.Số phát biểu đúng là A. 0 B. 1 C....
Đọc tiếp
Cho hàm số y = log 2 x . Xét các phát biểu
(1) Hàm số y = log 2 x đồng biến trên khoảng (0;+∞) .
(2) Hàm số y = log 2 x có một điểm cực tiểu.
(3) Đồ thị hàm số y = log 2 x có tiệm cận.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2
Đáp án D
Phương pháp:
Đánh giá từng đáp án.
Cách giải:
(1) Hàm số y = log2x đồng biến trên khoảng (0;+∞): đúng, do 2 > 1
(2) Hàm số y = log2x có một điểm cực tiểu: sai, hàm số y = log2x luôn đồng biến trên (0;+∞)
(3) Đồ thị hàm số y = log2x có tiệm cận: đúng, tiệm cận đó là đường x = 0
Số phát biểu đúng là 2.
Đúng 0
Bình luận (0)
Số nghiệm của phương trình
log
2
x
-
3
+
log
2
x
-
1
3
là A. 2. B. 3. C. 1. D. 0.
Đọc tiếp
Số nghiệm của phương trình log 2 x - 3 + log 2 x - 1 = 3 là
A. 2.
B. 3.
C. 1.
D. 0.