hình thoi có 3 cạnh à bạn, mk mới nghe đấy

ý mình là cho 1 cạnh bằng 3 cm ạ

 hình thoi có canh à

câu 2
Bài giải:
Chu vi hình bình hành là:
(6+5)x2= 22(cm)
Chiều cao hình bình hành là:
6x\(\dfrac{2}{3}\)= 4(cm)
Diện tích hình bình hành là:
6x4= 24(cm²)
      Đáp số: 22cm
                   24cm²

câu 3
bài giải:
Đường chéo thứ hai của mảnh vườn hình thoi dài là:
96x\(\dfrac{3}{8}\)= 36(m)
Diện tích mảnh vườn hình thoi dài là:
(96x36):2= 1728(m²) 
          Đáp số: 1728 m²

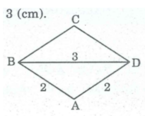
*Cách dựng:

- Dựng ∆ ABD biết AB = AD = 2(cm), BD = 3(cm).

- Trên nửa mặt phẳng bờ BD không chứa điểm A. Từ B dựng tia Bx // AD, từ D dựng tia DY // AB, chúng cắt nhau tại C.

Ta có hình thoi ABCD cần dựng

*Chứng minh:

Vì AB // CD và AD // BC nên tứ giác ABCD là hình bình hành

AB = AD = 2cm. Vậy tứ giác ABCD là hình thoi.

Lại có: BD = 3cm

Hình thoi dựng được thỏa mãn điều kiện bài toán.

Câu 1. S               Câu 2.Đ

Câu 3.S                Câu 4.Đ

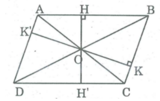
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm

* Kéo dài OH cắt cạnh CD tại H'.

Ta có OH ⊥ BC

⇒ OH' ⊥ CD và OH' = 2cm

Suy ra HH' bằng đường cao của hình bình hành.

S A B C D  = HH'.AB ⇒ 

* Kéo dài OK cắt AD tại K'.

Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)

Suy ra KK' là đường cao của hình bình hành.

S A B C D  = KK'.AB ⇒ 

Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).