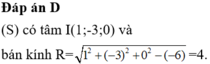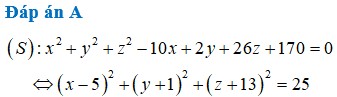Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0). Tính thể tích tứ diện SAB'C'

Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S): x²+y²+z²-2x+6y-6=0. Bán kính của (S) bằng:
A. √46
B. 16
C. 2
D. 4.
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
y
+
4
z
0
. Thể tích khối cầu (S) là A.
12
π
B.
36
π
C.
24
π
D.
25
π
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 y + 4 z = 0 . Thể tích khối cầu (S) là
A. 12 π
B. 36 π
C. 24 π
D. 25 π
Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 = 4 a 2 (a > 0).
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
+
4
y
-
4
0
Thể tích của khối cầu (S) bằng A.
36
π
B.
9
π
C.
32
π
D.
16...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 4 y - 4 = 0 Thể tích của khối cầu (S) bằng
A. 36 π
B. 9 π
C. 32 π
D. 16 π
Mặt cầu (S) có tâm I(1;-2;0), R=3
![]()
Chọn đáp án A.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
10
x
+
2
y
+
26
z
+
170
0
, tọa độ tâm của (S) là A. (5;-1;-13) B. (-5;1;13) C. (10;-2;-26) D. (-10;2;26)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0 , tọa độ tâm của (S) là
A. (5;-1;-13)
B. (-5;1;13)
C. (10;-2;-26)
D. (-10;2;26)
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
11...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Tọa độ tâm T của (S) là
A. T(2;4;6).
B. T(1;2;3).
C. T(-2;-4;-6).
D. T(-1;-2;-3).
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 3 = 0 . Bán kính mặ cầu bằng
A. 3
B. 4
C. 2
D. 5
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
2
z
-
4
y
-
6
z
0
.Tính diện tích mặt cầu(S). A.
42
π
B.
36
π
C.
9
π
D.
12
π
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 z - 4 y - 6 z = 0 .Tính diện tích mặt cầu(S).
A. 42 π
B. 36 π
C. 9 π
D. 12 π
Đáp án B
Ta có:
S : x - 1 2 + y - 2 2 ÷ z - 3 2 = 9 ⇒ S có bán kính R = 3
Diện tích mặt cầu (S) là: 4 π · 3 2 = 36 π .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 x - 4 y - 6 z = 0 . Tính diện tích mặt cầu (S).
A. 42 π
B. 36 π
C. 9 π
D. 12 π
Đáp án B
Ta có:
![]()
=> (S) có bán kính R =3
Diện tích mặt cầu là: 4 π . 3 2 = 36 π
Đúng 0
Bình luận (0)