Cho hình chóp S . A B C có đáy là A B C là tam đều cạnh a . Hình chiếu vuông góc của S lên A B C trùng với trung điểm H của cạnh B C . Biết tam giác S B C là tam giác đề. Tính số đo của góc giữa S A và A B C
A. 30 0
B. 75 0
C. 60 ∘
D. 45 0
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy là tam giác vuông tại A,
A
B
C
^
30
0
, SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là: A.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, A B C ^ = 30 0 , SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là:
A. a 3 3 9
B. a 3 18
C. a 3 3 3
D. a 3 12
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của S lên (ABC) là trung điểm của cạnh BC. Biết DSBC đều, tính góc giữa SA và (ABC) A.
60
°
B.
45
°
C.
90
°
D.
30
°
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của S lên (ABC) là trung điểm của cạnh BC. Biết DSBC đều, tính góc giữa SA và (ABC)
A. 60 °
B. 45 °
C. 90 °
D. 30 °
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S S trên đáy là điểm H nằm trên cạnh AC sao cho
A
H
2
3
A
C
, mặt phẳng (SBC) tạo với đáy một góc
60
0
.Tính thể tích khối chóp S. ABC A.
a
3
3...
Đọc tiếp
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S S trên đáy là điểm H nằm trên cạnh AC sao cho A H = 2 3 A C , mặt phẳng (SBC) tạo với đáy một góc 60 0 .Tính thể tích khối chóp S. ABC
A. a 3 3 12
B. a 3 3 36
C. a 3 3 24
D. a 3 3 8
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là
6
4
, từ B đến mặt phẳng (SAC) là
15
10
từ C đến mặt phẳng (SAB) là
30
20
và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng A.
1...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là 6 4 , từ B đến mặt phẳng (SAC) là 15 10 từ C đến mặt phẳng (SAB) là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
Cho hình chóp
S
.
A
B
C
có đáy
A
B
C
là tam giác đều cạnh bằng 1. Biết khoảng cách từ
A
đến mặt phẳng
S
B
C
là
6
4
, từ
B
đến mặt phẳng
S...
Đọc tiếp
Cho hình chóp S . A B C có đáy A B C là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng S B C là 6 4 , từ B đến mặt phẳng S A C là 15 10 ; từ C đến mặt phẳng S A B là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác A B C . Thể tích khối chóp S . A B C bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
Cho hình chóp
S
.
A
B
C
có đáy là tam giác đều cạnh
a
, hình chiếu vuông góc của đỉnh S trên đáy là điểm H nằm trên cạnh AC sao cho
A
H
2
3
A
C
, mặt phẳng (SBC) tạo với đáy một góc
60
0
.Tính thể tích khối chóp S.ABC A.
a
3
3
12...
Đọc tiếp
Cho hình chóp S . A B C có đáy là tam giác đều cạnh a , hình chiếu vuông góc của đỉnh S trên đáy là điểm H nằm trên cạnh AC sao cho A H = 2 3 A C , mặt phẳng (SBC) tạo với đáy một góc 60 0 .Tính thể tích khối chóp S.ABC
A. a 3 3 12
B. a 3 3 36
C. a 3 3 24
D. a 3 3 8
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi
B
1
,
C
1
lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A, B, C,
B
1
,
C
1
. A.
a
3
2...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A, B, C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi
B
1
,
C
1
lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A,B,C,
B
1
,
C
1
. A.
a
3
2
B.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A,B,C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Đáp án B.
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ I A = I B = I C (1).
Ta có ∆ S A C = ∆ S A B ⇒ A B 1 = A C 1 . Từ đây ta chứng minh được B 1 C 1 / / B C .
Gọi M là trung điểm của B C ⇒ B C ⊥ S A M ⇒ B 1 C 1 ⊥ S A M .
Gọi H = S M ∩ B 1 C 1 ⇒ H B 1 M B = H C 1 M C , do M B = M C nên H B 1 = H C 1
Mặt phẳng (SAM) đi qua trung điểm H của B 1 C 1 nên B 1 C 1 ⊥ S A M nên (SAM) là mặt phẳng trung trực của B 1 C 1 . Do I ∈ A M ⊂ S A M nên I B 1 = I C 1 (2).
Gọi N là trung điểm của AB, suy ra A B ⊥ I N S A ⊥ I N ⇒ I N ⊥ S A B .
Tam giác A B B 1 vuông tại B 1 có N là trung điểm của AB nên N A = N B 1 = 1 2 A B .
Như vậy ta có các tam giác vuông sau bằng nhau
∆ I N A = ∆ I N B = ∆ I N B 1 ⇒ I A = I B = I B 1 (3).
Từ (1), (2) và (3) suy ra 5 điểm A,B,C, B 1 , C 1 cùng nằm trên mặt cầu tâm I, bán kính R = I A = 2 3 . a 3 2 = a 3 3 (do ABC là tam giác đều và I là tâm đường tròn ngoại tiếp ⇒ I cũng là trọng tâm tam giác ABC).
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→ 2BH→, SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC A.
V
a
3
12
B.
V
a
3
7
12...
Đọc tiếp
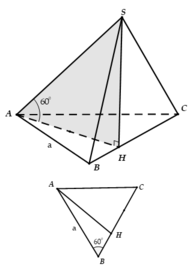
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→ = 2BH→, SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC
A. V = a 3 12
B. V = a 3 7 12
C. V = a 3 4
D. V = a 3 3 8
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→ 2BH→, (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC A.
V
a
3
3
24
B.
V
a
3...
Đọc tiếp
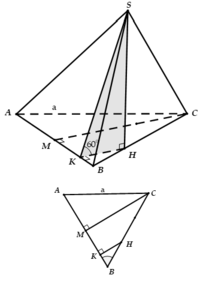
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→ = 2BH→, (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC
A. V = a 3 3 24
B. V = a 3 3 12
C. V = a 3 3 4
D. V = a 3 3 6
