Trong không gian Oxzy, cho đường thẳng d : x − 2 − 1 = y − 1 2 = z 1 . Đường thẳng d có vectơ chỉ phương là
A. u 3 → = 2 ; 1 ; 1
B. u 4 → = − 1 ; 2 ; 0
C. u 1 → = 1 ; − 2 ; − 1
D. u 2 → = 2 ; 1 ; 0
Những câu hỏi liên quan
Trong không gian Oxzy cho hai đường thẳng
d
1
:
x
+
1
3
y
−
1
2
z
−
2
−
1
,
d
2
:...
Đọc tiếp
Trong không gian Oxzy cho hai đường thẳng d 1 : x + 1 3 = y − 1 2 = z − 2 − 1 , d 2 : x − 1 − 1 = y − 1 2 = z + 1 − 1 . Đường thẳng ∆ đi qua điểm A 1 ; 2 ; 3 vuông góc với d 1 và cắt đường thẳng d 2 có phương trình là
A. x − 1 1 = y − 2 − 1 = z − 3 1
B. x − 1 1 = y − 2 − 3 = z − 3 − 3
C. x − 1 − 1 = y − 2 − 3 = z − 3 − 5
D. x − 1 2 = y − 2 − 1 = z − 3 4
Trong không gian với hệ tọa độ Oxzy, cho mặt phẳng
(
P
)
:
x
−
y
+
z
−
3
0
đường thẳng
Δ
:
x
−
1
1
y
2
z
+
2
−
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxzy, cho mặt phẳng ( P ) : x − y + z − 3 = 0 đường thẳng Δ : x − 1 1 = y 2 = z + 2 − 3 . Phương trình đường thẳng đi qua O song song với (P), vuông góc với đường thẳng ∆ là
A. x 1 = y − 4 = z 3
B. x − 1 1 = y − 4 4 = z − 3 3
C. x + 4 y + 3 z = 0
D. x − 4 y + 3 z = 0
Trong không gian với hệ tọa độ Oxzy, viết phương trình tham số của đường thẳng nằm trong mặt phẳng
y
+
2
z
0
và cắt hai đường thẳng
d
1
:
x
1
-
t
y
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxzy, viết phương trình tham số của đường thẳng nằm trong mặt phẳng y + 2 z = 0 và cắt hai đường thẳng d 1 : x = 1 - t y = t z = 4 t , d 1 : x = - t ' y = 4 + 2 t ' z = 1
A. x = 4 t y = - 2 t z = t
B. x = 1 + 4 t y = - 2 t z = t
C. x = 1 + 4 t y = 2 t z = t
D. x = 4 t y = 2 t z = t
Đáp án B
Gọi A, B lần lượt là giao điểm của (P) và d1; (P) và d2.
Ta tìm được A(1;0;0), B(5;-2;1)
Khi đó đường thẳng AB là đường thẳng cần tìm.
Vậy phương trình tham số của đường thẳng cần tìm là x = 1 + 4 t y = - 2 t z = t
Đúng 0
Bình luận (0)
rong không gian với hệ tọa độ Oxzy, cho đường thẳng
d
1
:
x
−
1
a
y
−
3
b
z
4
v
à
d
2
:
x
1
y...
Đọc tiếp
rong không gian với hệ tọa độ Oxzy, cho đường thẳng d 1 : x − 1 a = y − 3 b = z 4 v à d 2 : x 1 = y + 1 4 = z − 2 − 2 . Tổng a + b bằng bao nhiêu để d1//d2?
A. a + b = -10
B. a + b = 10
C. a + b = 6
D. không tồn tại
Đáp án D.
d1) đi qua điểm M1(1;3;0), có vecto chỉ phương là u → 1 = a ; b ; 4
(d2) đi qua điểm M2(0;-1;2), có vecto chỉ phương là u → 2 = 1 ; 4 ; − 2
Đúng 0
Bình luận (0)
Trong không gian Oxzy, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
6
x
+
4
y
-
2
z
+
10
0
và cho mặt phẳng
P
:
x
-
y
+
2
z
-
7...
Đọc tiếp
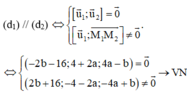
Trong không gian Oxzy, cho mặt cầu S : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 10 = 0 và cho mặt phẳng P : x - y + 2 z - 7 = 0 . Giả sử M ∈ P , N ∈ S sao cho MN song song với đường thẳng x - 5 1 = y + 2 1 = z - 4 2 . Khoảng cách giữa hai điểm M, N lớn nhất bằng bao nhiêu ?
A. 8 - 2
B. 2 - 2 2
C. 4 + 2 2
D. 6 - 2
Trong không gian tọa độ Oxyz, cho đường thẳng d:
x
-
1
2
y
+
1
-
1
z
+
2
-
2
. Điểm nào dưới đây KHÔNG thuộc đường thẳng...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho đường thẳng d: x - 1 2 = y + 1 - 1 = z + 2 - 2 . Điểm nào dưới đây KHÔNG thuộc đường thẳng d?
Thay lần lượt tọa độ các điểm vào phương trình đường thẳng ta thấy tọa độ của Q không thỏa mãn phương trình. Vậy điểm Q không thuộc đường thẳng d.
Chọn D
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
2
y
+
1
-
1
z
+
2
-
2
. Điểm nào dưới đây KHÔNG thuộc đường thẳng d? A....
Đọc tiếp
Trong không gian tọa độ Oxyz, cho đường thẳng d : x - 1 2 = y + 1 - 1 = z + 2 - 2 . Điểm nào dưới đây KHÔNG thuộc đường thẳng d?
A. M 3 ; - 2 ; - 4
B. 1 ; - 1 ; - 2
C. P - 1 ; 0 ; 0
D. Q - 3 ; 1 ; - 2
Đáp án D
Phương pháp:
Thay tọa độ các điểm vào phương trình đường thẳng và kiểm tra tọa độ đó có thỏa mãn phương trình hay không.
Cách giải
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho đường thẳng
d
:
x
-
2
-
1
y
-
1
2
z
1
. Đường thẳng d có một vectơ chỉ phương là: A.
u
1
⇀...
Đọc tiếp
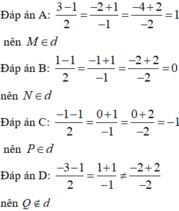
Trong không gian Oxyz, cho đường thẳng d : x - 2 - 1 = y - 1 2 = z 1 . Đường thẳng d có một vectơ chỉ phương là:
A. u 1 ⇀ = - 1 ; 2 ; 1
B. u 2 ⇀ = 2 ; 1 ; 0
C. u 3 ⇀ = 2 ; 1 ; 1
D. u 4 ⇀ = - 1 ; 2 ; 0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
−
1
2
y
1
z
+
1
−
2
. Trong các điểm dưới đây, điểm nào thuộc đường thẳng d? A. M(-1;0;1) B. N(3;1;1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x − 1 2 = y 1 = z + 1 − 2 . Trong các điểm dưới đây, điểm nào thuộc đường thẳng d?
A. M(-1;0;1)
B. N(3;1;1)
C. P(-1;-1;1)
D. Q(1;0;1)