Cho đồ thị hàm số y = f (x) như hình vẽ.
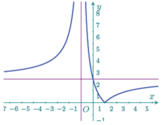
Xét các mệnh đề sau
I . lim x → + ∞ f x = 2
I I . lim x → − ∞ f x = − ∞
I I I . lim x → 1 − f x = 2
I V . lim x → 1 + f x = + ∞
Có bao nhiêu mệnh đề đúng?
A. 4
B. 3
C. 1
D. 2
Những câu hỏi liên quan
Cho hàm số f(x) có đạo hàm trên
ℝ
và có đồ thị yf(x) như hình vẽ. Xét hàm số
g
(
x
)
f
(
x
2
-
2
)
. Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (-1;0). B. Hàm số g(x) nghịch biến trên....
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên ℝ và có đồ thị y=f'(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (-1;0).
B. Hàm số g(x) nghịch biến trên. ( - ∞ ; - 2 )
C. Hàm số g(x) nghịch biến trên. ( 0 ; 2 )
D. Hàm số g(x) đồng biến trên. ( 2 ; + ∞ )
Cho hàm số yf(x) có đạo hàm trên R và có đồ thị yf’(x) như hình vẽ. Xét hàm số
g
(
x
)
f
(
x
2
-
2
)
Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2) B. Hàm số g(x) đồng biến trên (2;+∞) C. Hàm số g(x) nghịch biến trên (-∞;-2) D. Hàm số g(x) nghịch biến trên (-1;0)
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị y=f’(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 )
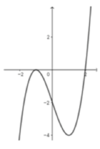
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+∞)
C. Hàm số g(x) nghịch biến trên (-∞;-2)
D. Hàm số g(x) nghịch biến trên (-1;0)
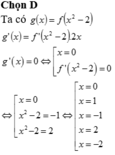
g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu g’(x)
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị y f(x) như hình vẽ. Xét hàm số g(x) f(
x
2
-2). Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2). B. Hàm số g(x) đồng biến trên (2;+
∞
). C. Hàm số g(x) nghịch biến trên (-
∞
;-2). D. Hàm số g(x) nghịch biến trên (-1;0).
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị y = f'(x) như hình vẽ.
Xét hàm số g(x) = f( x 2 -2).
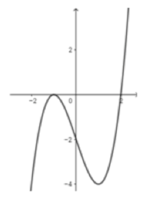
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2).
B. Hàm số g(x) đồng biến trên (2;+ ∞ ).
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2).
D. Hàm số g(x) nghịch biến trên (-1;0).
Chọn D
Ta có g(x) = f( x 2 -2).
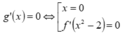
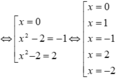
Ta có g'(3) = 6.f'(7) > 0, g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu g’(x):
Suy ra đáp án là D.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị của hàm số y f(x) như hình vẽ. Xét hàm số g(x) f
x
2
-
2
Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2) B. Hàm số g(x) đồng biến trên (2;+
∞
) C. Hàm số g(x) nghịch biến trên (-
∞
;-2) D. Hàm số g(x) nghịch biến trên (-1;0).
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị của hàm số y = f'(x) như hình vẽ. Xét hàm số g(x) = f x 2 - 2
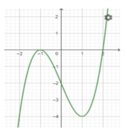
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+ ∞ )
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2)
D. Hàm số g(x) nghịch biến trên (-1;0).
Chọn D.
Xét g(x) = f x 2 - 2
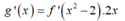
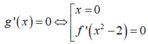
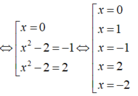
Bảng xét dấu g’(x):
Suy ra hàm số g(x) nghịch biến trên (-1;0) là sai.
Đúng 1
Bình luận (0)
Cho hàm số yf(x) có đạo hàm trên R và có đồ thị của hàm số yf (x) như hình vẽ. Xét hàm số
g
x
f
x
2
-
2
.Mệnh đề nào sau đây sai? A. Hàm số g(x) nghịch biến trên (0;2). B. Hàm số g(x) đồng biến trên
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị của hàm số y=f '(x) như hình vẽ. Xét hàm số g x = f x 2 - 2 .
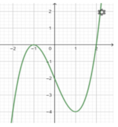
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2).
B. Hàm số g(x) đồng biến trên 2 ; + ∞
C.Hàm số g(x) nghịch biến trên - ∞ ; - 2
D. Hàm số g(x) nghịch biến trên (-1;0).
Cho hàm số yf(x) liên tục trên R, đồ thị của đạo hàm f(x) như hình vẽ sau:Trong các mệnh đề sau, mệnh đề nào sai? A. f đạt cực tiểu tại x0 B. f đạt cực tiểu tại x-2 C. f đạt cực đại tại x-2 D. cực tiểu của f nhỏ hơn cực đại.
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R, đồ thị của đạo hàm f'(x) như hình vẽ sau:
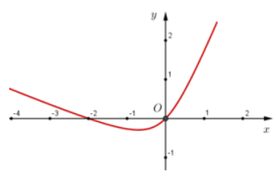
Trong các mệnh đề sau, mệnh đề nào sai?
A. f đạt cực tiểu tại x=0
B. f đạt cực tiểu tại x=-2
C. f đạt cực đại tại x=-2
D. cực tiểu của f nhỏ hơn cực đại.
Đáp án B
Quan sát đồ thị hàm số y = f ' x ta có:
f ' x > 0 ⇔ x < − 2 x > 0 , f ' x < 0 ⇔ − 2 < x < 0 ⇒ B sai; A,C và D đúng.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm trên
ℝ
và có đồ thị hàm số y f (x) như hình vẽ bên. Xét hàm số
g
x
f
x
3
-
2
Mệnh đề nào sau đây là sai? A. Hàm số g(x) nghịch biến trên khoảng (-1;0) B. Hàm số g(x) nghịch biến trên khoảng
-
∞
;
-...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên ℝ và có đồ thị hàm số y = f '(x) như hình vẽ bên. Xét hàm số g x = f x 3 - 2 Mệnh đề nào sau đây là sai?
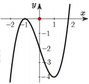
A. Hàm số g(x) nghịch biến trên khoảng (-1;0)
B. Hàm số g(x) nghịch biến trên khoảng - ∞ ; - 2
C. Hàm số g(x) nghịch biến trên khoảng (0;2)
D. Hàm số g(x) đồng biến trên khoảng 2 ; + ∞
Đáp án A.
Ta có g ' x = x 2 - 2 ' f ' x 2 - 2 = 2 x . f ' x 2 - 2 ; ∀ x ∈ ℝ .
Khi đó g ' x < 0 ⇔ x . f ' x 2 - 2 < 0 ⇔ [ x < 0 f ' x 2 - 2 > 0 x > 0 f ' x 2 - 2 < 0 ⇔ [ x < 0 x 2 - 2 > 2 x > 0 x 2 - 2 < 2 ⇔ [ 0 < x < 2 x < - 2 .
Vậy hàm số nghịch biến trên khoảng - ∞ ; - 2 và (0;2) khẳng định A là sai.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đồ thị yf’(x) như hình vẽ. Xét hàm số
g
x
1
3
x
3
+
3
4
x
2
-
3
2
x
-
f
x
mệnh đề nào dưới đây đúng? A.
m
a
x...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị y=f’(x) như
hình vẽ. Xét hàm số g x = 1 3 x 3 + 3 4 x 2 - 3 2 x - f x
mệnh đề nào dưới đây đúng?
A. m a x - 3 ; 1 g x = g - 3
B. m a x - 3 ; 1 g x = g - 1
C. m a x - 3 ; 1 g x = g 1
D. m a x - 3 ; 1 g x = g - 3 + g 1 2
Cho hàm số y f(x). Đồ thị hàm số đạo hàm y f(x) như hình vẽ dưới đây. Xét hàm số g(x) f(x) -
1
3
x
3
-
3
4
x
2
+
3
2
x
+
2018
. Mệnh đề nào dưới đây đúng? A.
m
i
n
[
-...
Đọc tiếp
Cho hàm số y = f(x). Đồ thị hàm số đạo hàm y = f'(x) như hình vẽ dưới đây. Xét hàm số g(x) = f(x) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 . Mệnh đề nào dưới đây đúng?
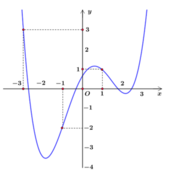
A. m i n [ - 3 ; 1 ] g ( x ) = g(1)
B. m i n [ - 3 ; 1 ] g ( x ) = g(-3)
C. m i n [ - 3 ; 1 ] g ( x ) = g ( - 3 ) + g ( 1 ) 2
D. m i n [ - 3 ; 1 ] g ( x ) = g(-1)
Chọn D
Xét hàm số g(x) = f(x) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 .
Cho 
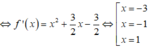
Dựa vào đồ thị ta so sánh được m i n [ - 3 ; 1 ] g ( x ) = g(-1)
Đúng 0
Bình luận (0)