Cho hai số phức z,w thỏa mãn z − 3 − 2 i ≤ 1 w + 1 + 2 i ≤ w − 2 − i . Tìm giá trị nhỏ nhất P m i n của biểu thức P = z − w .
A. P min = 3 2 − 2 2
B. P min = 3 2 + 2 2
C. P min = 2 + 1
D. P min = 5 2 − 2 2
Những câu hỏi liên quan
Cho hai số phức z, w thay đổi thỏa mãn
z
3
,
z
−
w
1
. Biết tập hợp điểm của số phức w là hình phẳng H. Tính diện tích S của hình H. A.
S
20
π
B.
S
12
π
C.
S
4
π
D.
S
16
π
Đọc tiếp
Cho hai số phức z, w thay đổi thỏa mãn z = 3 , z − w = 1 . Biết tập hợp điểm của số phức w là hình phẳng H. Tính diện tích S của hình H.
A. S = 20 π
B. S = 12 π
C. S = 4 π
D. S = 16 π
Phương pháp:
Sử dụng phương pháp hình học: Tìm tập hợp các điểm biểu diễn số phức z, w và tính toán.
Cách giải:
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
-
3
+
2
i
z
-
i
Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Đọc tiếp
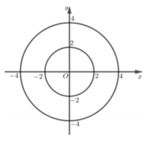
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Cho hai số phức z,w thỏa mãn |z+2w|4,|z-2w|2,|3z+w|3. Tìm giá trị của biểu thức P
z
¯
w
+
z
w
¯
.
A. 4 B. 3 C. 6 D. 9
Đọc tiếp
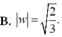
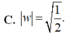
Cho hai số phức z,w thỏa mãn |z+2w|=4,|z-2w|=2,|3z+w|=3. Tìm giá trị của biểu thức P= z ¯ w + z w ¯ .
A. 4
B. 3
C. 6
D. 9
Cho hai số phức z,w thỏa mãn |z+2w|4,|z-2w|2,|3z+w|3. Tìm giá trị của biểu thức P
z
w
+
z
w
.
A. 4 B. 3 C. 6 D. 9
Đọc tiếp
Cho hai số phức z,w thỏa mãn |z+2w|=4,|z-2w|=2,|3z+w|=3. Tìm giá trị của biểu thức P= z w + z w .
A. 4
B. 3
C. 6
D. 9
Cho số phức z thỏa mãn
z
-
1
-
i
1
, số phức w thỏa mãn
w
¯
-
2
-
3
i
2
. Tìm giá trị nhỏ nhất của
z
-
w
.
Đọc tiếp
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tìm giá trị nhỏ nhất của z - w .
Cho số phức z thỏa mãn
z
−
1
−
i
1
, số phức w thỏa mãn
w
¯
−
2
−
3
i
2
. Tìm giá trị nhỏ nhất của
z
−
w
....
Đọc tiếp
Cho số phức z thỏa mãn z − 1 − i = 1 , số phức w thỏa mãn w ¯ − 2 − 3 i = 2 . Tìm giá trị nhỏ nhất của z − w .
A. 17 + 3
B. 13 + 3
C. 13 - 3
D. 17 - 3
Cho số phức z thỏa mãn
z
-
1
-
i
1
, số phức w thỏa mãn
w
¯
-
2
-
3
i
2
. Tính giá trị nhỏ nhất của
z
-
w...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Cho hai số phức z, w thỏa mãn
|
z
-
3
-
2
i
|
≤
1
|
w
+...
Đọc tiếp
Cho hai số phức z, w thỏa mãn | z - 3 - 2 i | ≤ 1 | w + 1 + 2 i | ≤ | w - 2 - i | . Tìm gía trị nhỏ nhất P m i n của biểu thức P = |z-w|.
A . P m i n = 3 2 - 2 2
B . P m i n = 2 + 1
C . P m i n = 5 2 - 2 2
D . P m i n = 2 2 + 1 2
Cho hai số phức z, w thỏa mãn
z
+
2
w
3
,
2
z
+
3
w
6
và
z
+
4
w
7
Tính giá trị của biểu thức
P
z...
Đọc tiếp
Cho hai số phức z, w thỏa mãn z + 2 w = 3 , 2 z + 3 w = 6 và z + 4 w = 7 Tính giá trị của biểu thức P = z . w ¯ + z ¯ . w
A. P=-14i
B. P=-28i
C. P=-14
D. P=-28
Cho hai số phức z, w thỏa mãn
z
−
3
−
2
i
≤
1
w
+
1
+...
Đọc tiếp
Cho hai số phức z, w thỏa mãn z − 3 − 2 i ≤ 1 w + 1 + 2 i ≤ w − 2 − i .
Tìm giá trị nhỏ nhất P min của biểu thức P = z − w .
A. P min = 3 2 − 2 2
B. P min = 2 + 1
C. P min = 5 2 − 2 2
D. P min = 2 2 + 1 2
Đáp án C
Đặt z = x + y i x , y ∈ ℝ ,
khi đó
z − 3 − 2 i ≤ 1 ⇔ x − 3 2 + y − 2 2 ≤ 1
Suy ra tập hợp điểm biểu diễn số phức z là miền trong đường tròn
x − 3 2 + y − 2 2 = 1.
Đặt w = a + b i a , b ∈ ℝ , khi đó w + 1 + 2 i ≤ w − 2 − i ⇔ a + b ≤ 0
Suy ra tập hợp điểm biểu diễn số phức w là miền x + y ≤ 0 , bờ là đường thẳng x + y = 0 .
Gọi C : x − 3 2 + y − 2 2 = 1 có tâm I 3 ; 2 , bán kính R = 1 và Δ : x + y = 0 .
Do đó
P = z − w = M N ⇒ M N min = d I ; Δ − R = 5 2 − 1 = 5 2 − 2 2 .
Đúng 0
Bình luận (0)