Trong không gian với hệ tọa độ O x y z , cho đường thẳng △ : x − 1 = y − 2 1 = z + 1 3 và mặt phẳng P : 11 x + m y + n z − 16 = 0 . Biết △ ⊂ P , Tính giá trị của T = m + n .
A. T = − 14.
B. T = − 2.
C. T = 2.
D. T = 14.
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t
Trong không gian với hệ trục tọa độ , cho bốn đường thẳng:
d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 ; d 2 : x 1 = y - 2 = z - 1 1
d 3 : x - 1 2 = y + 1 1 = z - 1 1 ; d 4 : x 1 = y - 1 - 1 = z - 1
Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0
B. 2
C. Vô số.
D. 1
Chọn A
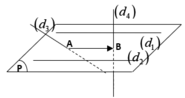
Ta có d1 song song d2, phương trình mặt phẳng chứa hai đường thẳng d1, d2 là
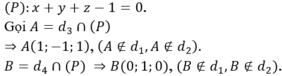
Mà ![]() cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 3 2 = y + 2 - 1 = z + 1 4 . Điểm nào sau đây không thuộc đường thẳng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng
D 1 : x − 2 1 = y + 2 − 1 = z − 1 − 1 ; D 2 : x − 1 1 = y − 1 2 = z − 1 ; D 3 : x − 1 = y + 2 1 = z + 1 1
và đường thẳng D 4 : x − 5 1 = y − a 3 = z − b 1 . Biết không tồn tại đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Tính giá trị của biểu thức T = a - 2b.
A. T = -2
B. T = -3
C. T = 2
D. T = 3
Đáp án C.
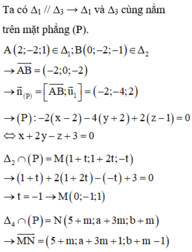
Không tồn tại đường thẳng nào trong không gian cắt cả 4 đường thẳng đã cho
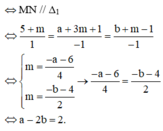
Trong không gian với hệ tọa độ Oxzy, cho mặt phẳng ( P ) : x − y + z − 3 = 0 đường thẳng Δ : x − 1 1 = y 2 = z + 2 − 3 . Phương trình đường thẳng đi qua O song song với (P), vuông góc với đường thẳng ∆ là
A. x 1 = y − 4 = z 3
B. x − 1 1 = y − 4 4 = z − 3 3
C. x + 4 y + 3 z = 0
D. x − 4 y + 3 z = 0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 1 - 1 = z - 3 3 . Đường thẳng d đi qua điểm M và có vectơ chỉ phương α d → có tọa độ là:
A. M 2 ; - 1 ; 3 , α d → = - 2 ; 1 ; 3
B. M 2 ; - 1 ; - 3 , α d → = 2 ; - 1 ; 3
C. M - 2 ; 1 ; 3 , α d → = 2 ; - 1 ; 3
D. M 2 ; - 1 ; 3 , α d → = 2 ; - 1 ; - 3
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 1 - 1 = z - 3 3 . Đường thẳng d đi qua điểm M và có vectơ chỉ phương α d → có tọa độ là:
A. M 2 ; - 1 ; 3 , α d → = - 2 ; 1 ; 3
B. M 2 ; - 1 ; - 3 , α d → = 2 ; - 1 ; 3
C. M - 2 ; 1 ; 3 , α d → = 2 ; - 1 ; 3
D. M 2 ; - 1 ; 3 , α d → = 2 ; - 1 ; - 3
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 1 - 1 = z - 3 3 . Đường thẳng d đi qua điểm M và có vectơ chỉ phương u → có tọa độ là:
A. M 2 ; - 1 ; 3 , u → - 2 ; 1 ; 3
B. M 2 ; - 1 ; - 3 , u → 2 ; - 1 ; 3
C. M - 2 ; 1 ; 3 , u → 2 ; - 1 ; 3
D. M 2 ; - 1 ; 3 , u → 2 ; - 1 ; - 3
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương u → 2 ; - 1 ; 3 .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x - 1 1 = y - 2 - 1 = z - 1 2 và mặt phẳng P : x + 2 y + z - 5 = 0 . Tọa độ giao điểm A của đường thẳng ∆ và mặt phẳng (P) là:
A. A(3;0;-1)
B. A(0;3;1)
C. A(0;3;-1)
D. A(-1;0;3)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: x + 1 3 = y - 1 - 2 = z - 2 1 .Đường thẳng d có một VTCP là:
A. a → = 1 ; - 1 ; - 2
B. a → = - 1 ; 1 ; 2
C. a → = 3 ; 2 ; 1
D. a → = 3 ; - 2 ; 1
Đáp án D
Phương pháp:
Đường thẳng d: x - x 0 a = y - y 0 b = z - z 0 c có 1 VTCP là a → = a ; b ; c
Cách giải: Đường thẳng d có 1 VTCP là a → = 3 ; - 2 ; 1