Tìm tọa độ điểm M trên trục Ox cách đều hai điểm A 1 ; 2 ; − 1 và điểm B 2 ; 1 ; 2
A. M 1 2 ; 0 ; 0
B. M 3 2 ; 0 ; 0
C. M 2 3 ; 0 ; 0
D. M 1 3 ; 0 ; 0
Tìm tọa độ điểm M trên trục Ox cách đều hai điểm A(1;2;-1) và điểm B(2;1;2)
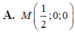


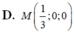
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C. M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2
Chọn C.
Do điểm M thuộc trục Ox nên M(a,0,0)
Vì M cách đều hai điểm A, B nên MA = MB hay
![]()
![]()
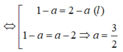
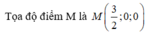
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C. M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2
Chọn C.
Do điểm M thuộc trục Ox nên M(a,0,0)
Vì M cách đều hai điểm A, B nên MA = MB hay
![]()
![]()
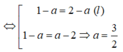
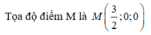
Cho các điểm A(-3; 2), B(1; 4). Điểm M trên trục Ox cách đều A và B có tọa độ là
A. M 1 2 ; 0
B. M - 1 2 ; 0
C. M 3 2 ; 0
D. M(4; 0)
Cho hai điểm A(3; -1) và B( 0;3) Tìm tọa độ điểm M trên trục Ox sao cho khoảng cách từ M đến đường thẳng AB bằng AB?
A.(0; -4)
B. (2; 0) và (1; 0)
C. (4; 0)
D.Đáp án khác
Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5
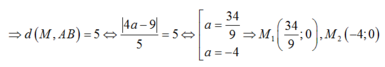
Trong không gian tọa độ Oxyz, cho hai điểm A(1;-1;0) và B(1;2;-3). Tọa độ điểm M nằm trên trục Oz và cách đều hai điểm A, B là
A. M(0;0;-3)
B. M(0;0;-1)
C. M(0;0;-2)
D. M(0;0;2)
1) Cho hàm số y=0,5x-2 có đồ thị (d).
a. Tính góc tạo bởi (d) và trục Ox.
b. Tìm trên (d) những điểm cách đều 2 trục tọa độ.
2) Cho (d): y=mx-m+2. Tính khoảng cách lớn nhất từ điểm M(6;1) đến (d).
Trong không gian tọa độ Oxyz cho các điểm: A(1; -3; -1); và B(-2; 1; 3)
a) Chứng tỏ rằng hai điểm A và B cách đều trục Ox.
b) Tìm điểm C nằm trên Oz sao cho tam giác ABC vuông tại C.
c) Viết phương trình hình chiếu của đường thẳng AB trên mp(Oyz).
d) Viết phương trình mặt cầu đi qua ba điểm O, A, B và có tâm nằm trên mp(Oyz).
a) \(Ox:\left\{{}\begin{matrix}x=t\\y=0\\z=0\end{matrix}\right.\).
Lấy điểm \(M\left(1;0;0\right)\in Ox\).
\(d\left(A,Ox\right)=\dfrac{\left|\left[\overrightarrow{MA},\overrightarrow{u_{Ox}}\right]\right|}{\left|\overrightarrow{u_{Ox}}\right|}=\sqrt{10}\).
\(d\left(B,Ox\right)=\dfrac{\left|\left[\overrightarrow{MA},\overrightarrow{u_{Ox}}\right]\right|}{\left|\overrightarrow{u_{Ox}}\right|}=\sqrt{10}\)
Do đó hai điểm \(A,B\) cách đều trục \(Ox\).
b) Điểm \(C\in Oz\) nên tọa độ điểm \(C\) có dạng \(\left(0;0;c\right)\).
Tam giác \(ABC\) vuông tại \(C\) nên \(CA\perp CB\)
suy ra \(\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow1.\left(-2\right)-3.1-\left(1+c\right).\left(3-c\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}c=-2\\c=4\end{matrix}\right.\).
c) Mặt phẳng \(\left(Oyz\right)\): \(x=0\).
Hình chiếu của \(A,B\) trên \(\left(Oyz\right)\) lần lượt là \(A'\left(0;-3;-1\right)\), \(B'\left(0;1;3\right)\).
Phương trình hình chiếu của đường thẳng \(AB\) trên \(\left(Oyz\right)\) là phương trình của đường thẳng \(A'B'\).
d) Gọi tọa độ tâm thỏa mãn yêu cầu bài toán là \(I\left(0;a;b\right)\).
Có \(IO=IA=IB\) suy ra
\(a^2+b^2=1^2+\left(a+3\right)^2+\left(b+1\right)^2=2^2+\left(a-1\right)^2+\left(b-3\right)^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-47}{16}\\b=\dfrac{53}{16}\end{matrix}\right.\).
Trong không gian tọa độ Oxyz, cho hai điểm A 1 ; - 1 ; 0 và B 1 ; 2 ; - 3 . Tọa độ điểm M nằm trên trục Oz và cách đều hai điểm A, B là
A. M(0;0;-3)
B. M(0;0;-1)
C. M(0;0;-2)
D. M(0;0;2)