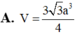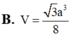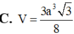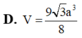Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, SA = 2a và SA vuông góc với mặt đáy (ABCD). Biết AD = 2a, AB = BC = CD = a. Diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD bằng bao nhiêu?
![]()
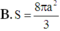
![]()
![]()
Đáp án A

ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
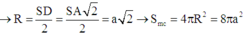
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với đáy lớn AD = 2a, AB = BC = a. Cạnh bên SA vuông góc với mặt phẳng đáy, SA = a 2 . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. R = a 6 3
B. R = a 2 2
C. R = a 3 2
D. R = a 6 2
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D. AB=2AD, AD=DC, BC=a√2. ∆SBC cân tại S và nằm trong mặt phẳng vuông góc với đág. SA hợp với đáy 1 góc 45°. Tính d(SA;BC)
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với AD = 2a, AB = BC = a, SA ⊥ (ABCD), SA = a 2 . Tính thể tích V của hình chóp S.ABD.
A. V = a 3 2 3
B. V = a 3 3 6
C. V = a 3 3
D. V = a 3 6
Cho hình chóp S.ABCD có đáy là hình thang cân với đáy AB=2a, AD=BC=CD=a, mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ A tới mặt phẳng (SBC) bằng 2 a 15 5 , tính theo a thể tích V của khối chóp
A. V = 3 a 3 3 4
B. V = 3 a 3 4
C. V = 3 a 3 5 4
D. V = 3 a 3 2 4
Cho hình chóp S.ABCD có đáy là hình thang cân với đáy A B = 2 a , A D = B C = C D = a , mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ A tới mặt phẳng (SBC) bằng 2 a 15 5 , tính theo a thể tích V của khối chóp
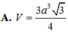
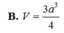
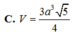
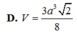
Cho khối chóp S.ABCD có đáy ABCD là hình thang cân với đáy AD và BC. Biết AD=2a, AB=BC=CD=a Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AD thỏa mãn HD=3HA , SD tạo với đáy một góc 45 o .Tính thể tích V của khối chóp S.ABCD