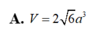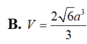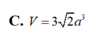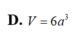Cho hình hộp chữ nhật ABCD.A'B'C'D' có A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
A. V = 2 6 a 3
B. V = 2 6 a 3 3
C. V = 3 2 a 3
D. V = 6 a 3
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có các kích thước là a , b , c ( a < b < c ) . Hình hộp chữ nhật này có mấy mặt đối xứng
A. 1
B. 2
C. 3
D. 4
Chọn C.
Hình hộp chữ nhật ABCD.A’B’C’D’ có 3 mặt đối xứng, đó là các mặt phẳng trung trực AB, AD, AA’.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AC' = 6 a. Thể tích khối hộp chữ nhật ABCD.A'B'C'D' bằng:
A. 3 a 3 3
B. 2 a 3 3
C. 2 a 3
D. 2 3 a 3
Phương pháp:
Công thức tính thể tích khối hộp chữ nhật ABCD.A'B'C'D' là V = AA'.AB.AD
Cách giải:
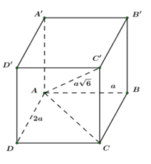
Ta có: ![]() (định lý Pitago)
(định lý Pitago)
Xét tam giác ACC’ vuông tại C ta có:
![]()
![]()
![]()
Chọn C.
Oxyz cho hình hộp ABCd.a'b'c'd' a(1.1.1) b(2.-1.3)d(5.2.0)a'(-1.3.1).sac ding C. b ' và ABCd là hình chữ nhật
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=2a, BC=a. Biết bán kính của mặt cầu ngoại tiếp của hình hộp chữ nhật là 3a/2. Thể tích của hình hộp chữ nhật là:
A. a 3 3 2
B. 4 a 3
C. 2 a 3
D. 2 3 a 3
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AD=2a, AA'=3a. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là
![]()
![]()
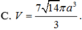
![]()
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
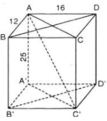
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒ 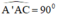
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
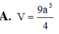
![]()
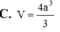
![]()
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD= 2 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'