Tìm số điểm cực trị của hàm số y = f x biết f ' x = x x 2 − 1 x + 2 2018 .
A.2
B.3
C.4
D.1
Những câu hỏi liên quan
Cho hàm số y f(x). Hàm số y f (x) có đồ thị như hình bên.Tìm số điểm cực trị của hàm số y f(x). A. 3 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y = f(x). Hàm số y = f ' (x) có đồ thị như hình bên.
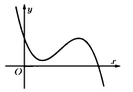
Tìm số điểm cực trị của hàm số y = f(x).
A. 3
B. 1
C. 0
D. 2
Đáp án B.
f ' (x) đổi dấu 1 lần, suy ra hàm số y = f(x) có 1 điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Biết rằng hàm số yf(x) có m điểm cực trị, hàm số
y
f
(
x
)
có n điểm cực trị, hàm số
y
f
x
có p điểm cực trị. Giá trị m+n+p là A. 26 B. 30 C. 27 D. 31
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng hàm số y=f(x) có m điểm cực trị, hàm số
y
=
f
(
x
)
có n điểm cực trị, hàm số
y
=
f
x
có p điểm cực trị. Giá trị m+n+p là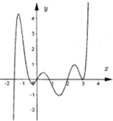 
A. 26
B. 30
C. 27
D. 31
Cho hàm sốy=f(x). Hàm số y=f’(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y=f(x)
A. 0
B. 1
C. 2
D. 3
Đáp án B
Nhìn vào đồ thị hàm số ta thấy có một giá trị của x (gải sử x = a) để y’=0 và không có giá trị nào của x làm y’ không xác định. Mặt khác y' đổi dấu từ dương sang âm khi đi qua x = a do vậy x = a là một điểm cực trị của hàm số y=f(x).
Ta chọn B
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm là f(x)
x
-
2
4
(
x
-
1
)
(
x
+
3
)
x
2
+
3
. Tìm số điểm cực trị của hàm số y f(x) A. 6. B. 3. C. 1. D. 2.
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f''(x) = x - 2 4 ( x - 1 ) ( x + 3 ) x 2 + 3 . Tìm số điểm cực trị của hàm số y = f(x)
A. 6.
B. 3.
C. 1.
D. 2.
Đáp án là D
Hàm số f(x) có đạo hàm là
f''(x) = 0 
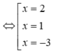
Bảng biến thiên
Từ BBT ta thấy hàm số có 2 điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm sốyf(x) . Hàm số yf(x) có bảng biến thiên như hình vẽ sau:Tìm số điểm cực trị của hàm số: yf(x).
Đọc tiếp
Cho hàm sốy=f(x) . Hàm số y=f'(x) có bảng biến thiên như hình vẽ sau: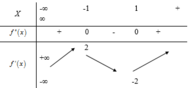
Tìm số điểm cực trị của hàm số: y=f(x).
Cho hàm sốyf(x) . Hàm số yf(x)có bảng biến thiên như hình vẽ sau:Tìm số điểm cực trị của hàm số: yf(x). A. 0. B. 1 C. 2. D. 3.
Đọc tiếp
Cho hàm sốy=f(x) . Hàm số y=f'(x)có bảng biến thiên như hình vẽ sau:
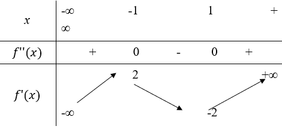
Tìm số điểm cực trị của hàm số: y=f(x).
A. 0.
B. 1
C. 2.
D. 3.
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = - 2017 ( x - 1 ) ( x + 2 ) 3 ( x - 3 ) 2 Tìm số điểm cực trị của f(x)
A. 3
B. 2
C. 0
D. 1
Đáp án B
Ta có y , = 0 ⇔ x = 1 x = - 2 x = 3 , y , đổi dấu qua x=1 và x=-2 , y , không đổi dấu qua x=3 nên hàm số có hai cực trị tại x=1 và x=-2
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm là
f
x
x
-
2
4
x
-
1
x
+
3
x
2
+
3
. Tìm số điểm cực trị của hàm số yf(x) A. 1. B. 2. C. 6...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm là f ' x = x - 2 4 x - 1 x + 3 x 2 + 3 . Tìm số điểm cực trị của hàm số y=f(x)
A. 1.
B. 2.
C. 6.
D. 3.
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 2 , ∀ x ∈ ℝ . Tìm số điểm cực trị của hàm số đã cho
A. 3
B. 2
C. 4
D. 1
Cho hàm số yf(x) liên tục trên K có đạo hàm f(x) Đồ thị của hàm số f(x) như hình vẽ bên. Tìm số điểm cực trị của đồ thị hàm số f(x)? A. 3 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) liên tục trên K có đạo hàm f'(x) Đồ thị của hàm số f'(x) như hình vẽ bên.
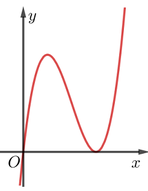
Tìm số điểm cực trị của đồ thị hàm số f(x)?
A. 3
B. 1
C. 0
D. 2
Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
Đúng 0
Bình luận (0)