Cho các số phức z, z1, z2 thay đổi thỏa mãn các điều kiện sau: i z + 2 i + 4 = 3 ; phần thực của z1 bằng 2; phần ảo của z2 bằng 1. Tìm giá trị nhỏ nhất của biểu thức T = z - z 1 2 + z - z 2 2
A. 9
B. 2
C. 5
D. 4
Cho các số phức z , z 1 , z 2 thay đổi thỏa mãn các điều kiện sau: i z + 2 i + 4 = 3 ; phần thực của z 1 bằng 2; phần ảo của z 2 bằng 1. Tìm giá trị nhỏ nhất của biểu thức T = z - z 1 2 + z - z 2 2
A. 9
B. 2
C. 5
D. 4
Cho các số phức z 1 = - 2 + i , z 2 = 2 + i và số phức z thay đổi thỏa mãn z - z 1 2 + z - z 2 2 = 16 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Giá trị biểu thức M 2 - m 2 bằng
A. 15
B. 7
C. 11
D. 8
Tìm mô đun của số phức w = z 3 + z + 1 z 2 + 1 biết rằng số phức z thỏa mãn điều kiện z + z 1 + i + z - z 2 + 3 i = 4 - i
A. 170 10
B. 171 10
C. 172 10
D. 173 10
Gọi z = a + bi với a , b ∈ ℝ
Khi đó phương trình z + z 1 + i + z - z 2 + 3 i = 4 - i trở thành:
2 a 1 + i + 2 b 2 + 3 i = 4 - i ⇔ 2 a + 4 b + 2 a + 6 b i = 4 - i
Do đó:
2 a + 4 b = 4 2 a + 6 b = - 1 a = 1 2 b = - 1 2 ⇒ z = 1 2 - 1 2 i
Ta có: w = z 3 + z + 1 z 2 + 1 - = z + 1 z 2 + 1 Thay 1 2 - 1 2 i vào ta được:
w = 1 2 - 1 2 i + 1 1 2 - 1 2 i 2 + 1 = 1 2 - 1 2 i + 1 - 1 2 i + 1 = 13 10 - 1 10 i
Suy ra w = 13 10 2 + - 1 10 2 = 170 10
Đáp án A
Cho z 1 , z 2 là hai trong các số phức z thỏa mãn điều kiện |z - 5 – 3i| = 5, đồng thời z 1 - z 2 = 0 . Tập hợp các điểm biểu diễn của số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình nào dưới đây?
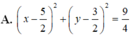
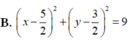
![]()
![]()
Giả sử M, N là điểm biểu diễn số phức z 1 , z 2 theo giả thiết suy ra M, N nằm trên đường tròn tâm I(5;3) bán kính r = 5 và MN là dây cung có độ dài bằng 8. Do đó trung điểm A của MN nằm trên đường tròn tâm I bán kính r' = 3.

Chọn C.
Cho z 1 , z 2 là hai trong các số phức z thỏa mãn điều kiện z - 5 - 3 i = 5 , đồng thời z 1 - z 2 = 8 . Tập hợp các điểm biểu diễn của số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình nào dưới đây?
A. x - 5 2 2 + y - 3 2 2 = 9 4
B. x - 5 2 2 + y - 3 2 2 = 9
C. x - 10 2 + y - 6 2 = 36
D. x - 10 2 + y - 6 2 = 16
Chọn C.
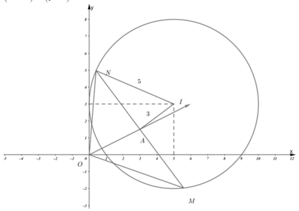
Phương pháp: Sử dụng phép biến hình.
Cách giải: Giả sử M, N là điểm biểu diễn số phức z 1 , z 2 theo giả thiết suy ra M, N nằm trên đường tròn tâm I(5;3) bán kính r = 5 và MN là dây cung có độ dài bằng 8. Do đó
trung điểm A của MN nằm trên đường tròn tâm I bán kính r' = 3.


Cho số phức z=1+i. Biết rằng tồn tại các số phức z 1 = a + 5 i , z 2 = b (trong đó a , b ∈ R , b > 1 ) thỏa mãn 3 | z - z 1 | = 3 | z - z 2 | = | z 1 - z 2 | . Tính b-a.
A. b - a = 5 3
B. b - a = 2 3
C. b - a = 4 3
D. b - a = 3 3
Kí hiệu A là tập hợp các số phức z đồng thời thỏa mãn hai điều kiện z - 1 = 34 và z + 1 + m i = z + m + 2 i (trong đó m ϵ R ). Gọi z 1 ; z 2 là hai số phức thuộc tập hợp A sao cho z 1 - z 2 là lớn nhất. Khi đó, hãy tính giá trị của z 1 + z 2
A. z 1 + z 2 = 10
B. z 1 + z 2 = 2
C. z 1 + z 2 = 2
D. z 1 + z 2 = 130
Cho z 1 , z 2 là hai số phức thỏa mãn điều kiện z - 5 - 3 i = 5 đồng thời z 1 - z 2 = 8 . Tập hợp các điểm biểu diễn số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình
A. x - 10 2 + y - 6 2 = 36
B. x - 10 2 + y - 6 2 = 16
C. x - 5 2 2 + y - 3 2 2 = 9
D. x - 5 2 2 + y - 3 2 2 = 9 4
Cho z 1 , z 2 là hai số phức thỏa mãn điều kiện |z-5-3i|=5 đồng thời z 1 - z 2 = 8 . Tập hợp các điểm biểu diễn số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy là đường tròn có phương trình
A. x - 10 2 + y - 6 2 = 36
B. x - 10 2 + y - 6 2 = 16
C. x - 5 2 2 + y - 3 2 2 = 9
D. x - 5 2 2 + y - 3 2 2 = 9 4
Tập hợp điểm biểu diễn số phức z=x+yi thỏa mãn |z-5-3i|=5 là đường tròn tâm I(5;3) bán kính R=5
Gọi M 1 ( x 1 ; y 1 ) ; M 2 ( x 2 ; y 2 ) là hai điểm biểu diễn các số phức z 1 ; z 2 thì từ z 1 - z 2 = 8 ta suy ra M 1 M 2 = 8
Gọi N(x;y) là điểm biểu diễn số phức w = z 1 + z 2 thì x = x 1 + x 2 y = y 1 + y 2
Gọi M là trung điểm M 1 M 2 thì M x 1 + x 2 2 ; y 1 + y 2 2
Ta có:
![]()
hay 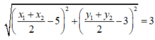
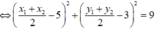
![]()
![]()
Vậy tập hợp các điểm N thỏa mãn bài toán là đường tròn
![]() .
.
Chọn đáp án A.