Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng A B C , A C = A D = 4 , A B = 3 , B C = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD)
A. d = 12 34
B. d = 60 769
C. d = 769 60
D. d = 34 12
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng ( A B C ) , A C = A D = 4 , B C = 5 . Tính khoảng cách d từ điểm A đến mặt phẳng (BCD)
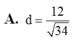
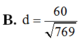
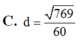
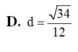
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC=AD=4,AB=3, BC=5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
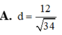
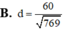
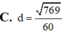
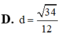
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC),AC =AD = 4, AB =3, BC = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
A. d = 12 34
B. d = 60 769
C. d = 769 60
D. d = 34 12
Đáp án A
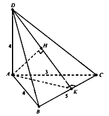
Vì B C 2 = B A 2 + A C 2 nên ∆ A B C vuông tại A.
Gọi K là hình chiếu của A lên BC, H là hình chiếu của A lên DK.
Ta có 1 A H 2 = 1 A D 2 + 1 A K 2 = 1 A D 2 + 1 A B 2 + 1 A C 2
= 1 4 2 + 1 4 2 + 1 3 2 = 17 72 ⇒ d A ; A B C D = A H = 72 17 = 12 34
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD = a, AC = 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện A B C D có DA vuông góc với mặt phẳng ( A B C ) và A D = a , A C = 2 a , cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện A B C D .
![]()
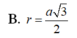
![]()
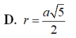
Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D và nằm trong mặt phẳng vuông góc với (ABC). Biết AD hợp với mặt phẳng (ABC) một góc 60°. Tính thể tích V của khối tứ diện ABCD.
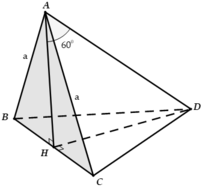
A. V = a 3 3 6
B. V = a 3 12
C. V = a 3 3 8
D. V = a 3 3 24
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Đáp án B
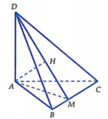
Ta có A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong (ABC) kẻ AM vuông góc tại M ⇒ 1 A M 2 = 1 A B 2 + 1 A C 2
Trong (DAM) kẻ A H ⊥ D M tại H.
Ta có
D A ⊥ B C ; A M ⊥ B C ⇒ D A M ⊥ B C ⇒ D A M ⊥ D B C
D A M ⊥ D B C D A M ∩ D B C = D M A H ⊂ D A M ; A H ⊥ D M ⇒ A H ⊥ D B C
⇒ d A ; D B C = A H
Tam giác DAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 A M 2 + 1 A D 2 = 1 A B 2 + 1 A C 2 + 1 A D 2 = 1 3 2 + 1 4 2 + 1 4 2 = 17 72 ⇒ A H = 12 34
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và α là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng với hình chóp S.ABCD là
A. S = a 2
B. S = 3 a 2 2
C. S = a 2 2
D. S = 2 a 2
Đáp án A.
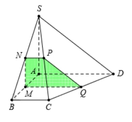
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .