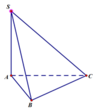
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh A; S A ⊥ A B C và S A = a 3 . Tính góc giữa đường thẳng SB với mặt phẳng (ABC)
A. 75 °
B. 60 °
C. 45 °
D. 30 °
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Tính thể tích khối chóp S.ABC.
A. a 3 3 12
B. a 3 4
C. a 3 3 4
D. a 3 12
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Tính thể tích khối chóp S.ABC
A. V = a 3 3 12
B. V = a 3 4
C. V = a 3 3 4
D. V = a 3 12
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, S A ⊥ ( A B C ) và S A = a 6 . Thể tích của khối chóp S.ABC bằng:
A. a 3 2 4
B. a 3 2
C. a 3 3 12
D. a 3 2 12
Đáp án A
Do tam giác ABC đều cạnh a nên có S ∆ A B C = a 2 3 4
⇒ V = 1 3 S A . S ∆ A B C = 1 3 . a 6 . a 2 3 4 = a 2 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA ⊥ (ABC) và SA= a 3 . Tính thể tích khối chóp S.ABC
A. 2 a 3 3
B. a 3 2
C. a 3 4
D. 3 a 3 4
Chọn C.

Diện tích ∆ ABC là S A B C = a 2 3 4
SA ⊥ (ABC) nên SA là chiều cao của hình chóp và SA= a 3
Thể tích khối chóp là
V = 1 3 S A B C . S A = 1 3 . a 2 3 4 . a 3 = a 3 4
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên S A ⊥ A B C và S A = a 3 . Tính thể tích khối chóp S.ABC
A. a 3 3
B. 3 a 3 4
C. a 3 4
D. 2 a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
A. a 3 6
B. a 3 3
C. a 3 8
D. 2 a 3
Đáp án C
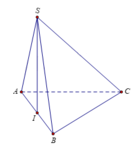
Gọi I là trung điểm của A B ⇒ S I ⊥ A B C
Ta có S I = a 2 − a 2 2 = a 3 2 ; S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích của khối chóp S . A B C là:
V = 1 3 S I . S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, cạnh bên SB vuông góc với đáy (ABC), SB = 2a. Tính thể tích khối chóp S.ABC.
A. a 3 3 6
B. a 3 3 2
C. a 3 4
D. 3 a 3 4
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V khối cầu ngoại tiếp hình chóp S.ABC
A. V = 4 3 π a 3 27
B. V = 5 15 π a 3 54
C. V = 5 15 π a 3 18
D. V = 5 π a 3 3
Đáp án B
Ta có: O là giao điểm của trục đường tròn ngoại tiếp tam giác ABC và SAB.
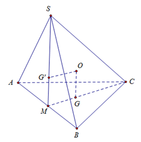
Ta có: O G = 1 3 S M = 3 6 ; M G = C M 3 = 3 6
R = S O = M G 2 + S G 2 = 3 6 + 1 3 = 15 6
Cách 2: Áp dụng CT giải nhanh trong trường hợp S A B ⊥ A B C ta có:
R 2 = R 2 A B C + R 2 S A B − A B 2 4 = 1 2 3 + 1 2 3 − 1 4 = 2 3 − 1 4 = 5 12 ⇒ R = 15 6 .
Vậy V = 4 3 π R 3 = 5 15 π 54 .
Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên tạo với đáy một góc 45 0 . Tính thể tích V của khối chóp S.ABC.
![]()