Cho π α > π β , với α , β ∈ ℝ . Mệnh đề nào dưới đây là đúng?
A. α > β
B. α < β
C. α = β
D. α ≤ β
Cho 0 < a ≠ 1 , α , β ∈ ℝ . Trong các mệnh đề sau, mệnh đề nào đúng?
A. a α a β = a α β
B. a α = a α a > 0
C. a α β = a α β
D. a α = a α
Cho 0 < a ≠ 1 ; α , β ∈ ℝ . Trong các mệnh đề sau, mệnh đề nào đúng?
A. a α a β = a α β
B. a a = a α a > 0
C. a α β = a α β
D. a α = a α
Cho 0 < a ≠ 1 , α , β ∈ ℝ . Trong các mệnh đề sau, mệnh đề nào đúng?
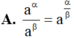
![]()
![]()
![]()
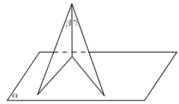
Cho ba mặt phẳng (α), (β), (γ), những mệnh đề nào sau đây đúng?
a) Nếu (α) ⊥ (β) và (α) // (γ) thì (β) ⊥ (γ).
b) Nếu (α) ⊥ (β) và (α) ⊥ (γ) thì (β) // (γ).
a) Đúng.
(α) ⊥ (β) ⇒ ∃ đường thẳng d ⊂ (β) và d ⊥ (α ).
Mà (α ) // (γ)
⇒ d ⊥ (γ)
⇒ (β) ⊥ (γ).
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.
Cho P = sin(π + α).cos(π - α) và Q = sin π 2 - α . cos π 2 + α .Mệnh đề nào dưới đây là đúng ?
A. P – Q = 1
B. P + Q = 2
C. P + Q = 0
D. P – Q = 0
Chọn C.
Ta có :
P = sin(π + α).cos(π - α) = -sin α.(-cos α) = sin α.cos α.
Và ![]() = cos α.(-sin α) = -sin α.cos α.
= cos α.(-sin α) = -sin α.cos α.
Do đó; P + Q = 0.
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Cho sinα = 8/17, sinβ = 15/17 với 0 < α < π/2, 0 < β <π/2. Chứng minh rằng: α + β = π/2
Hình vẽ sau là đồ thị của ba hàm số y = x α , y = x β , y = x γ (với x>0 ) và α , β , γ là các số thực cho trước.
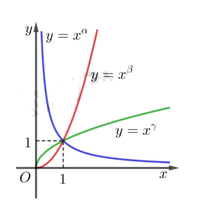
Mệnh đề nào dưới đây đúng?
C. α > β > γ
D. β > γ > α
Đáp án D
Hàm số x α nghịch biến do đó 0 < α < 1 .
Các hàm số x β , x γ là các hàm số đồng biến do đó β , γ > 1 .
Cho x = 100 ⇒ 100 β > 100 γ ⇒ β > γ .
Giả sử f x là một hàm số bất kỳ liên tục trên khoảng α ; β và a , b , c , b + c ∈ α ; β . Mệnh đề nào sau đây sai?
A. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x
B. ∫ a b f x d x = ∫ a b + c f x d x - ∫ c b f x d x
C. ∫ a b f x d x = ∫ a c f x d x + ∫ b + c b f x d x
D. ∫ a b f x d x = ∫ a c f x d x - ∫ b c f x d x
+) Đáp án A:
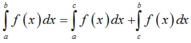
đáp án A đúng.
+) Đáp án C:
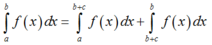
đáp án C đúng.
+) Đáp án D:
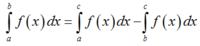
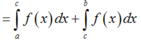
đáp án D đúng.
Chọn B.