Hàm số y = f(x) có giới hạn l i m x → a - f x = + ∞ và đồ thị (C) của hàm số y = f(x) chỉ nhận đường thẳng d làm tiệm cận đứng. Khẳng định nào sau đây đúng?
A. d: y = a
B. d: x = a
C. d: x = -a
D. d: y = -a
Cho hàm số y = f ( x ) , y = g ( x ) liên tục trên đoạn [ a ; b ] ( a < b ) . Hình phẳng D giới hạn bởi đồ thị hai hàm số y = f ( x ) , y = g ( x ) và hai đường thẳng x = a, x= b có diện tích là
A. S D = ∫ a b f ( x ) − g ( x ) d x .
B. S D = ∫ a b f ( x ) − g ( x ) d x .
C. S D = π ∫ a b f ( x ) − g ( x ) d x .
D. S D = ∫ b a f ( x ) − g ( x ) d x .
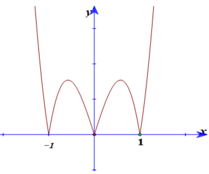
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7 15
B. 8 15
C. 14 15
D. 16 15
+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 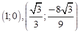 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
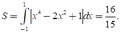
Chọn D.
Cho hàm số y = f(x) xác định và liên tục trên đoạn [-3;3] và có đồ thị như hình vẽ. Biết rằng diện tích hình phẳng S 1 , S 2 giới hạn bởi đồ thị hàm số y = f(x) và đường thẳng y = - x - 1 lần lượt là M;m. Tích phân ∫ - 3 3 f x d x bằng
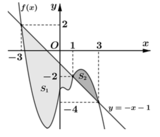
A. 6+m-M
B. 6-m-M
C. M-m+6
D. m-M-6
Cho hàm số y = f(x) liên tục trên [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(X), trục hoành và hai đường thẳng x = a; x = b (a<b) là
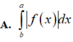
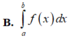
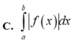
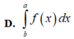
Cho hàm số y = f (x) liên tục trên
[ a ;b ]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a, x = b( a < b) là:
A. ∫ b a f x d x
B. ∫ a b f x d x
C. ∫ a b f x d x
D. ∫ b a f x d x
Đáp án C
Phương pháp: Sử dụng công thức ứng dụng tích phân để tính diện tích hình phẳng.
Cách giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) , trục hoành và hai đường thẳng x = a , x = b a < b là S = ∫ a b f x d x
Xét hàm số y = f(x) liên tục trên miền D = [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x = a; x = b Người ta chứng minh được rằng độ dài đường cong S bằng ∫ a b 1 + ( f ' ( x ) ) 2 d x Theo kết quả trên, độ dài đường cong S là phần đồ thị của hàm số f(x) = ln x và bị giới hạn bởi các đường thẳng x = 1 ; x = 3 là m - m + ln 1 + m n với m , n ∈ R thì giá trị của m 2 - m n + n 2 là bao nhiêu?
A. 6
B. 7
C. 3
D. 1
Cho hàm số y = f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức
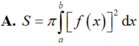
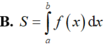
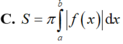

Chọn D
Hàm số y = f(x) liên tục trên [a; b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức S = ∫ a b f x d x .
Cho hàm số y = f(x) liên tục trên [a;b] Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x) trục hoành và hai đường thẳng x=a; x=b được tình theo công thức.
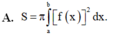
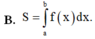
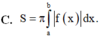
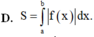
Cho hàm số y = f(x) liên tục trên [a;b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x=a, x=b được tình theo công thức.
A. S = π ∫ a b f x 2 d x .
B. S = ∫ a b f x d x .
C. S = π ∫ a b f x d x .
D. S = ∫ a b f x d x .