Tính thể tích của khối lập phương ABCD A'B'C'D' biết AD'=2a
A. V = a 3
B. V = 8 a 3
C. V = 2 2 a 3
D. V = 2 2 3 a 3
Thể tích V của khối hộp chữ nhật ABCD. A ' B ' C ' D ' biết A B = a ; A D = 2 a ; A C ' = a 14 là
A. V = 6 a 3
B. V = a 3 14 3
C. V = a 3 5
D. V = 2 a 3
Cho hình lập phương ABCD. A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và DCC'D'. Mặt phẳng (A'MN) chia khối lập phương trình hai phần có thể tích là V₁ và V₂ (V₁ < V₂). Tính tỷ số V₂/V₁
A. 5/2
B. 5/3
C. 3/2
D. 2
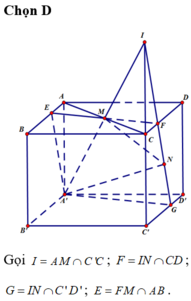
Vậy thiết diện của hình hộp cắt bởi mặt phẳng (A'MN) là hình bình hành A'EFG.
Ta có:
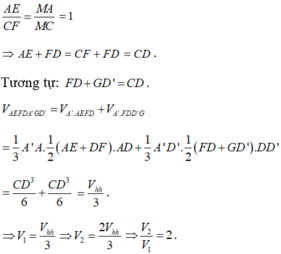
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. V = 18 a 3
B. V = 54 a 3
C. V = 12 a 3
D. V = 36 a 3
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. 12 a 3
B. 36 a 3
C. 54 a 3
D. 18 a 3
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. V = 12 a 3
B. V = 6 3 a 3
C. V = 2 3 a 3
D. V = 9 3 a 3
Đáp án là B

Gọi x là độ dài của cạnh hình lập phương
Ta có: 

Theo giả thiết, 
![]()
Vậy thể tích lập phương là: ![]()
Cho khối lập phương ABCD A'B'C'D' Người ta dùng 12 mặt phẳng phân biệt (trong đó, 4 mặt song song với (ABCD), 4 mặt song song với (AA'B'B)và 4 mặt song song với (AA'D'D)), chia khối lập phương nhỏ rời nhau và bằng nhau. Biết rằng tổng diện tích tất cả các khối lập phương nhỏ bằng 480. Tính độ dài a của khối lập phương ABCD A'B'C'D'
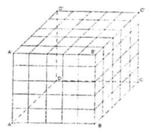
A. a=2
B. a = 2 3 .
C. a = 2 5 .
D.a=4
Đáp án D
Diện tích toàn phần của hình lập phương cạnh a là S t p = 6 a 2 .
Khi dùng các mặt phẳng như đề bài cho để chia khối lập phương ABCD.A’B’C’D’ ta được 125 khối lập phương nhỏ bằng nhau.
Do đó diện tích toàn phần của 1 khối lập phương nhỏ là 480 125 = 96 25
Gọi cạnh hình lập phương ABCD.A’B’C’D’ bằng a thì độ dài cạnh hình lập phương nhỏ bằng a 5 .
Suy ra diện tích toàn phần của 1 hình lập phương nhỏ là: 6 a 5 2 = 96 25 ⇔ a = 4
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a3
C. a 3 12
D. a 3 24
Chọn D
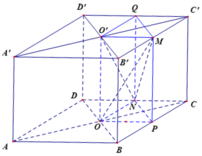
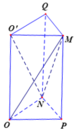
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có A B = a , A D = 2 a , B C = a . Biết rằng S A = a 2 . Tính thể tích V của khối chóp S.ABCD theo a.
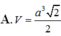
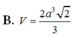
![]()
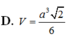
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có A B = a , A D = 2 a , B C = a . Biết rằng S A = a 2 Tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 3 2 2
B. V = 2 a 3 2 3
C. V = 2 a 2 3
D. V = a 3 2 6