Tất cả các giá trị thực của m để bất phương trình ( 3 m + 1 ) 18 x + ( 2 - m ) 6 x + 2 x < 0 có nghiệm đúng ∀ x > 0 là
A. ( - ∞ ; 2 )
B. - 2 ; - 1 3
C. - ∞ ; - 1 3
D. ( - ∞ ; - 2 ]
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Tìm tất cả các giá trị thực của tham số m để bất phương trình mx^2 + (m-1)x +m -1
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 5 x - 1 . log 2 2 . 5 x - 2 ≥ m có nghiệm x ≥ 1
A. m ≥ 6
B. m > 6
C. m ≤ 6
D. m < 6
Đáp án C.
Bất phương trình ⇔ log 2 5 x - 1 1 + log 2 5 x - 1 ≥ m
Đặt t = log 2 5 x - 1 , do x ≥ 1 ⇒ t ∈ [ 2 ; + ∞ )
Bất phương trình t 2 + t ≥ m ⇔ f ( t ) ≥ m
Với f ( t ) = t 2 + t , f ' ( t ) = 2 t + 1 > 0 với t ∈ [ 2 ; + ∞ ) nên hàm số f ( t ) đồng biến nên min ( t ) = f ( 2 ) = 6
Do đó theo bài ra để bất phương trình có nghiệm x ≥ 1 thì m ≤ min f ( t ) ⇔ m ≤ 6
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình 3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11.
B. m ≥ -11.
C. m < -11.
D. m ≤ -11.
Chọn A.
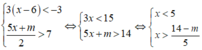
Hệ bất phương trình có nghiệm
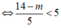 ⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
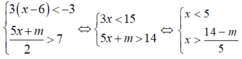
Hệ bất phương trình có nghiệm 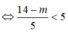
hay 14 - m < 25 hay m > -11
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
Ta có:
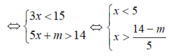
Hệ bất phương trình có nghiệm ⇔ 14 - m 5 < 5
Hay 14 - m < 25 tương đương m > -11
Tìm tất cả các giá trị thực của m để bất phương trình ( x 2 - 1 ) ( x - 1 ) x 3 + ( x 2 – x ) 2 ( 2 - m ) + ( x 2 - 1 ) ( x - 1 ) ≥ 0
A. m ≤ 2
B. m ≤ - 1 4
C. m ≤ 6
D. m ≤ 1
Gọi S là tập tất cả các giá trị của m để bất phương trình m x 2 + 6 < x + m nghiệm đúng với mọi giá trị thực của x. Khi đó, tập S là
A. S = − ∞ ; − 1 .
B. S = − ∞ ; 1 .
C. S = − ∞ ; − 30 5 .
D. S = − ∞ ; 30 5 .
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình x - 3 < 0 m - x < 1 vô nghiệm.
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Chọn D
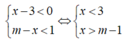
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4
Tìm tất cả các giá trị thực của tham số m để bất phương trình log2( 5x - 1) .log2)( 2.5x - 2) > m - 1 có nghiệm x ≥ 1?
A. m ≥ 7
B. m > 7
C. m ≤ 7
D. m < 7