Diện tích hình phẳng giới hạn bởi hai đường cong y = x 2 và y = 2 - x bằng
A. 5 2
B. 2
C. 7 3
D. 7 6
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
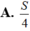
![]()
![]()
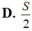
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
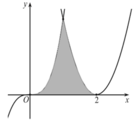
Diện tích hình phẳng giới hạn bởi parabol y= ( x - 2 ) 2 , đường cong y= x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
A. 11 2
B. 73 12
C. 7 12
D. 5 2
Chọn đáp án C.
Phương trình hoành độ giao điểm:
![]()
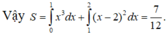
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
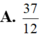
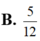
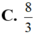
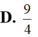
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
A . 37 12
B . 5 12
C . 8 3
D . 9 4
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong y = x 3 - x v à y = x - x 2
A. S= 12/37
B. S= 37/12
C. S= 9/4
D. S= 19/6
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong y = x 3 - x v à y = x - x 2
A. S= 12/37
B. S= 37/12
C. S= 9/4
D. S= 19/6
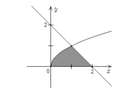
Cho (H) là hình phẳng giới hạn bởi đường cong y = x , trục hoành và đường thẳng y=2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng
A. 4 2 - 1 3
B. 7 6
C. 8 2 + 3 6
D. 5 6
Diện tích hình phẳng giới hạn bởi các đường cong y = sin x; y= cos x và các đường thẳng x = 0 , x = π bằng
A. 3 2
B. 2
C. 2 2
D. - 2 2
Đáp án C
Giải phương trình: s inx = cos x ⇒ x = π 4 (vì 0 ≤ x ≤ π )
S = ∫ 0 π s inx − cos x d x = 2 2