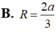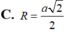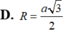Bán kính của mặt cầu ngoại tiếp chóp đều S.ABC có tất cả cac cạnh bằng a là:
A . 3 a 6 4
B . a 6 12
C . a 6 4
D . a 6 4
Bán kính của mặt cầu ngoại tiếp hình
chóp đều S.ABC có tất cả các cạnh
bằng a là
![]()
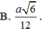
![]()
![]()
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc tạo bởi cạnh bên với đáy bằng 60 ° . Bán kính R mặt cầu ngoại tiếp hình chóp S.ABC là
A. R = a 2
B. R = 2 a 3
C. R = a 3 3
D. R = 4 a 3
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp.
A. R = a
B. R = a 2
C. R = a 2 2
D. R = a 3 2
Cho hình chóp S.ABC có SA= a 3 2 , các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là:
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có S A = a 3 2 , các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là:
A. R = a 13 2
B. R = a 3
C. R = a 13 3
D. R = a 13 6
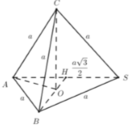
Ta có C A = C B = C S = a Hình chiếu của C trên (SAB) trùng với tâm đường tròn ngoại tiếp ∆ S A B .
Gọi O là tâm đường tròn ngoại tiếp ∆ S A B ⇒ S O ⊥ S A B .
Gọi H là trung điểm của SA. Tam giác SAB cân tại B ⇒ B H ⊥ S A ⇒ O ∈ B H .
Ta có:
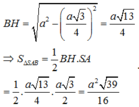
Gọi R là bán kính ngoại tiếp
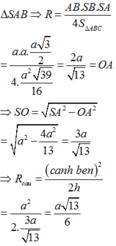
Chọn D.
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC, biết các cạnh đáy có độ dài bằng a, cạnh bên S A = a 3 .
A. 2 a 3 2
B. 3 a 3 2 2
C. a 3 8
D. 3 a 6 8
Chọn D.
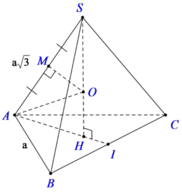
Gọi H là tâm của tam giác đều ABC, ta có SH⊥(ABC) nên SH là trục của tam giác ABC.
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA = OB = OC
Suy ra: O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC. Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có 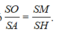
Ta có:
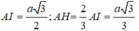
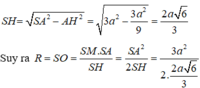
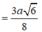
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên (SBC) vuông góc với đáy và C S B ^ = 90 o . Tính theo a bán kính mặt cầu ngoại tiếp chóp S.ABC?
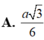
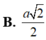
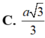
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên (SBC) vuông góc với đáy và C S B ^ = 90 o . Tính theo a bán kính mặt cầu ngoại tiếp chóp S.ABC
A. a 3
B. a 3 2
C. a 3 3
D. a 3 6
Hình chóp tam giác đều S.ABC, △ A B C đều cạnh a, đường cao SH=a. Tính bán kính R của mặt cầu ngoại tiếp S.ABC
![]()